经济学原理
第二章 偏好与选择
2.1 幸福与价值
人的最终目的是幸福,直接服务于这个最终目的是手段。
幸福:个人的全面发展,既包括个人生理性欲望和社会性欲望的满足,也包括个人潜能的开发。
幸福是一个主观观念,幸福需要物质支撑
2.1.1 目的与手段
- 假说1:人的行动是有目的的,行动只是实现某种目的的手段,没有目的的行动是不存在的。
2.1.2 幸福的时间维度和空间维度
- 👔幸福的时间维度:
一般来说,越是理性的人,越是注重行动的长远后果。
正是由于人们追求的是一生的幸福,而非短期的快乐,人们才愿意选择“先苦后甜”的生活方式。
正因为如此,人们才有可能为了一个好名声而牺牲眼前利益,愿意帮助他人,讲诚信,讲道德,而不是采取损人利己的机会主义行为。
😅人类有一个基本的倾向:对未来的、远处的东西看得轻,对眼前的、近处的东西看得重
🐒时间贴现
时间贴现:偏向目前本性所作决策对未来收入、幸福产生负面影响。
贴现因子:下一期的单位收入相当于目前收入的数值。
贴现率:目前单位收入比下一期单位货币折现到当前多出的比率。
贴现因子与贴现率关系:一个人越看重未来,贴现因子越大,对应贴现率越小;反之亦然。
贴现公式:
$$ σ = \dfrac{1}{1+r} $$
r:贴现率
σ:贴现因子
- 🍇幸福的空间维度:
人的幸福维度取决于多因素。
幸福维度:心理、社会、精神、物质财富。
2.1.3 价值
经济学上讲的价值:对实现目中目的的贡献的度量。
价值:对幸福这一最终目标的边际贡献。
一个物品或行动的价值量是由其对幸福的边际贡献决定的。如果一件物品或一个行动能增加人的幸福感,我们就说它是有价值的,否则,就是没有价值的。
边际贡献:指工具变量(物品或行动)变化一个单位会对目的变量造成的影响;没有影响:边际贡献 (价值)= 0 ,反之对生活产生影响,则价值为正,边际贡献为正,是稀缺品(价值>0)。
幸福是一种主观判断,因而价值也是一个主观概念,所以同样的物品或行动对不同的人具有不同的价值。
2.2 个人偏好和约束条件
🧍♂️偏好:对某种物品或行动的喜爱或厌恶倾向,某样东西可满足人的某种欲望。
人类的缺陷: 更重视看得见的东西,倾向于关注结果,忽略过程的价值。
2.2.1 功利主义幸福观
现在的主流经济学仍然建立在功利主义的基础上。
含义:人们追求的是情感和欲望的满足。(趋利避害 :最大化个人的快乐、最小化个人的痛苦)
个人功利主义:个体选择某种手段追求效用最大化。手段的价值,完全由其对个人效用的贡献决定。
社会功利主义:社会的目的是社会总福利的最大化。
功利主义完全是后果主义的:结果比动机手段更重要。只要目的正当,任何手段都是正当的。
社会功利主义弊端:忽视个人的基本权利,为专制主义和集体主义提供借口。
权力主义:个体的基本权利必须得到尊重,任何以“集体利益”的名义剥夺个人权利的行为都是不正当的,目的的正当性不能证成手段的正当性。
经济学认为,如果一个人是理性的,他的偏好必须满足两个公理,即完备性公理和一致性公理。
完备性公理: 任何两个可选择的方案之间都是可以比较的。
一致性公理(传递性公理):如果一个人认为A比B要好,B比C要好,一定会认为A比C要好。如果不满足这个假设,认为A比B好、B比C好,但又认为C比A好,说明这个人不理性。
偏好的主观性维度:生理、心理、家庭出身、社会环境、个人经验、观念、哲学、意识形态等。
经济学对偏好分析的缺陷:不分析人的偏好是如何形成和变化的。
2.2.2 效用函数
- 效用:偏好满足程度的度量。
- 效用函数:$u(x)$,自变量代表商品组合变量
偏好与满足偏好的手段之间的关系,表明消费变化如何影响所带来的价值量变化。
✍️$u(A)=4,u(B)=2$,表示消费者偏好于组合A而不是组合B,并不表示A的效用是B的效用的2倍。效用函数值是序数(ordinal)概念,而不是基数(cardinal)概念。
设想只有酒和面包两种消费品,一个酗酒成性的人,只要组合A比B有更多酒,A就严格好于B,而不论A和B中的面包为多少;只有当两个组合具有同等数量的酒时,他才偏好于包含更多面包的组合。
2.2.3 边际效用递减法则
边际效用:增加一单位产品的消费所带来的效用的增量。
大部分商品消费量饱和前,人们总偏好于较多的消费量,随着消费量增加,人们对再增加的一单位消费的欲望随之降低。新增加一单位消费所增加的效用会小于前一单位消费所增加的效用。边际效用递减法则:随着消费量的增加,产品的边际效用递减。
人们在做选择时,总先满足最迫切的用途,再满足次迫切的用途,最后再满足不迫切的用途。如果生活中只有一盆水,首先保证饮用数量,水的数量继续增多,可用来洗脸,再多一些,可用来洗澡、洗衣服,再多一些就可以用来浇花园。理性人不会把仅有的一瓶水拿去浇花园。这就是边际效用递减法则的行为学基础。
如果一种商品可以低成本地大量生产,一定不稀缺,所以它的价格也卖得很低。
- 效用的不可加总性:效用是主观的,效用值也具有任意性,不同人之间的效用不可比较,因而是不可加总的。
2.2.4 选择的约束条件:
技术性约束:技术上不可能。(时间、永动机、长生不老)
制度性约束:人类通过制度规则对自己施加约束。(产权、机票、收入) 制度本身来自技术约束。
道德性约束:人类通过道德规则施加的约束。
信息约束: 缺乏足够的信息而带来的约束。
2.3 鲁滨孙经济学
2.3.1 劳动与休闲之间的选择
鲁滨逊经济:生产者和消费者合二为一的个体经济,没有交换介入。
休闲:能够直接带来快乐的时间(当然在现实中,劳动和休闲很难严格区分)
技术约束:时间有限(劳动、休息、休闲)
边际成本:增加一单位产品的生产(或消费)所付出的代价或放弃的收益。
边际成本递增原因:
- 随着产量的增加,采摘更多的椰子变得越来越困难(理性的鲁滨孙一定会从最容易采摘的椰子开始采摘)
- 随着劳动时间的增加,单位劳动时间的疲劳程度会随之增加(包括体能的消耗和厌烦),或者说休闲时间的减少导致单位时间休闲的价值越来越高。
边际净收益:每增加1单位椰子带来的净效用的变化
- 净收益 = 总效用 - 总成本
- 边际净收益 = 边际效用 -边际成本
最优决策规则 最优选择在边际效用等于边际成本时达到。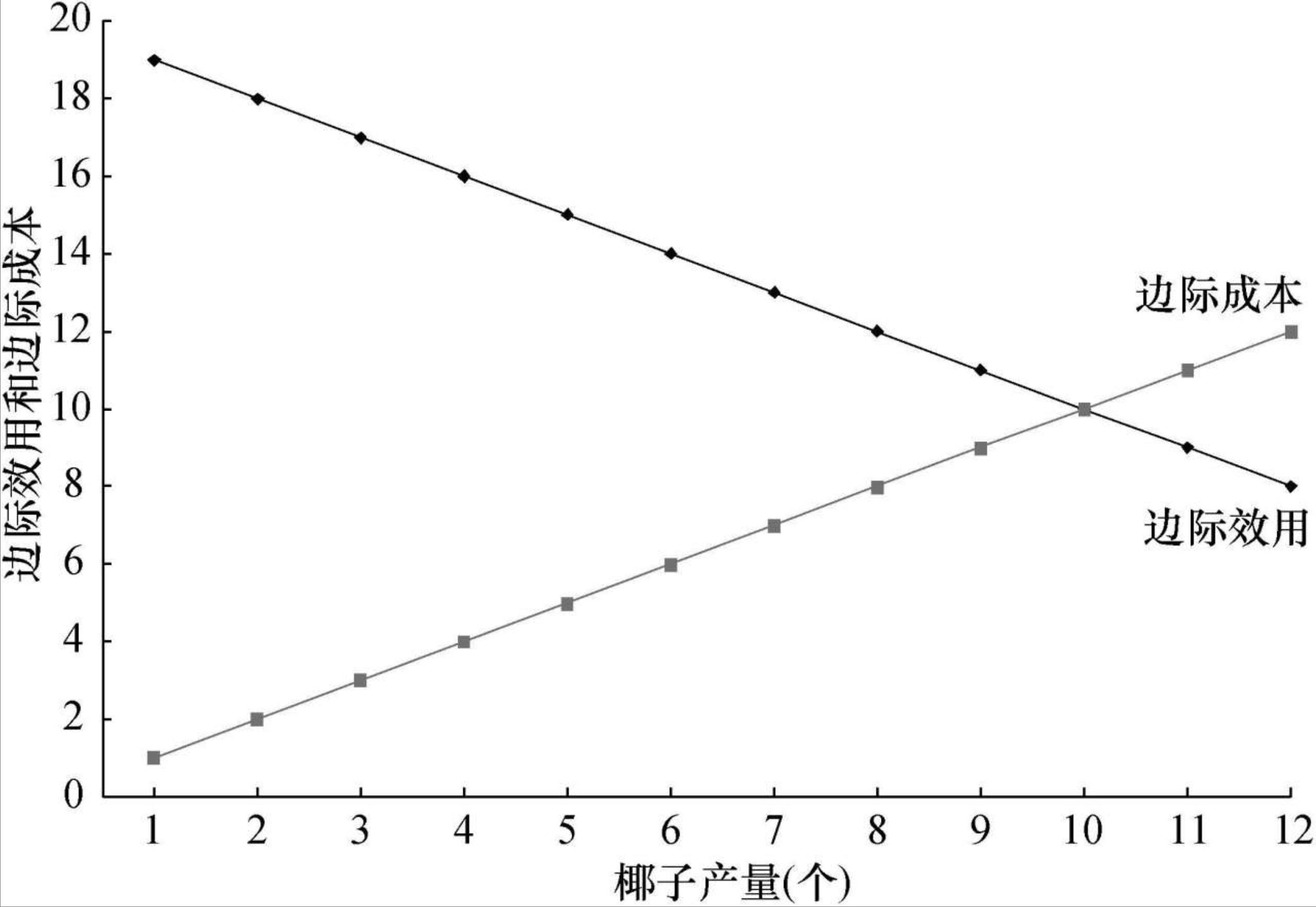
最优产量在总效用曲线和总成本曲线之间的距离最大时达到,此时边际效用等于边际成本。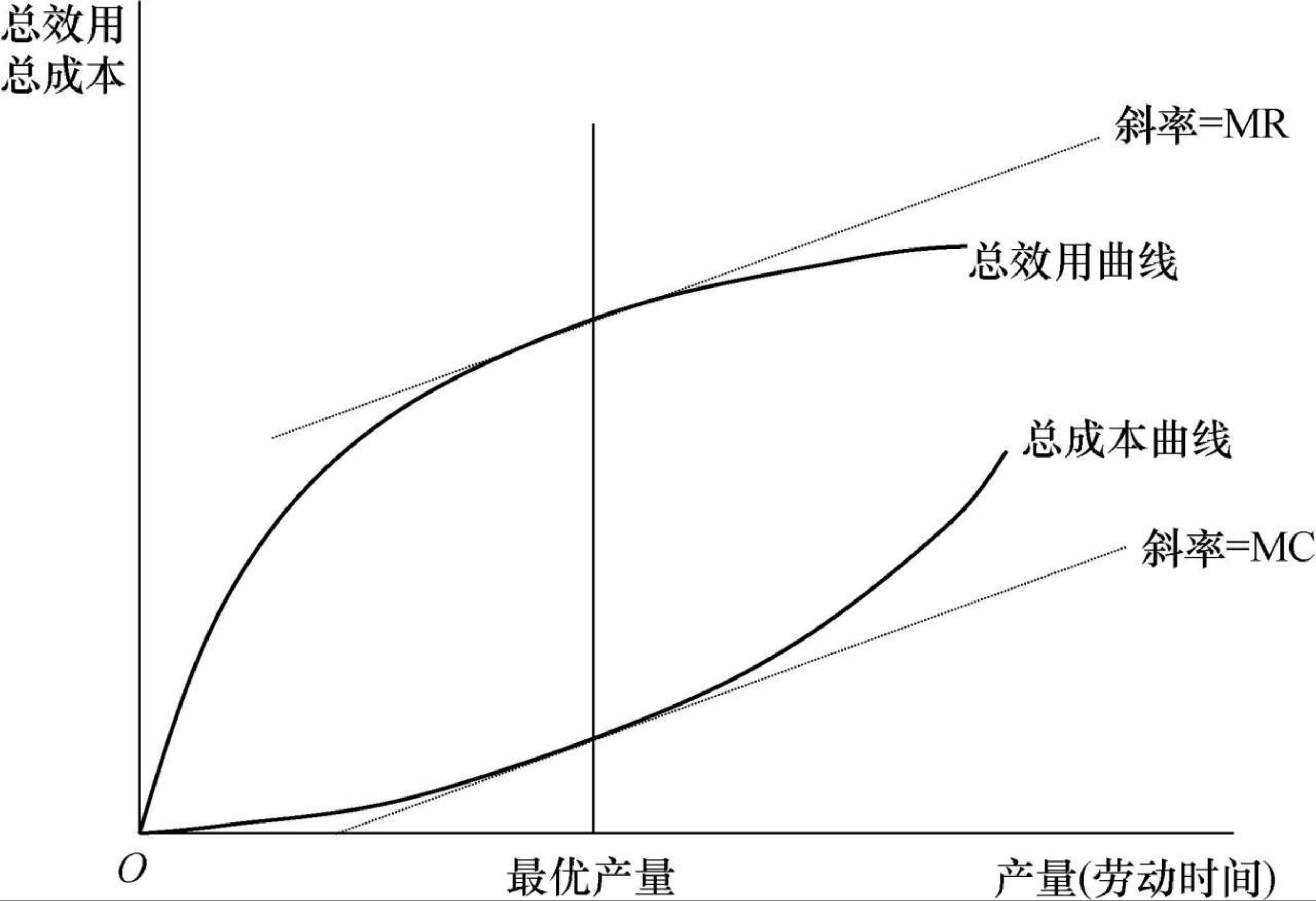
2.3.2 储蓄与投资
🌮储蓄=收入-消费
收入:一定时期内生产的可用于消费和投资的产品总量
消费:直接满足个人偏好的产品消耗
储蓄:为了投资和防患于未然而不用于消费的收入
资本品:人创造的、不能直接由大自然赐予的生产要素 (提高效率的工具、杠杆等)
生产要素:生产产品需要各种投入,包括劳动、资本品、土地和其他自然资源
投资:将储蓄转化为资本品的活动,目的是提高未来的生产率
折旧:资本品在使用过程中因磨损导致的价值损失
经济增长:单位时间内生产率的提高和可用于消费的产品的持续增加
2.4鲁滨孙经济的多元化
2.4.1 无差异曲线
无差异组合:不同的商品组合,人们从中得到的效用程度相同
无差异曲线:无差异组合连成的曲线,给定相同效用水平的所有产品组合点的连线,反映了不同产品在偏好上的可替代性。
边际替代率递减法则:维持同一效用水平的前提下,随着某商品消费量增加,该产品能够替代的其他商品的消费量将随之递减。
- 鱼和椰子的边际效用都是正:
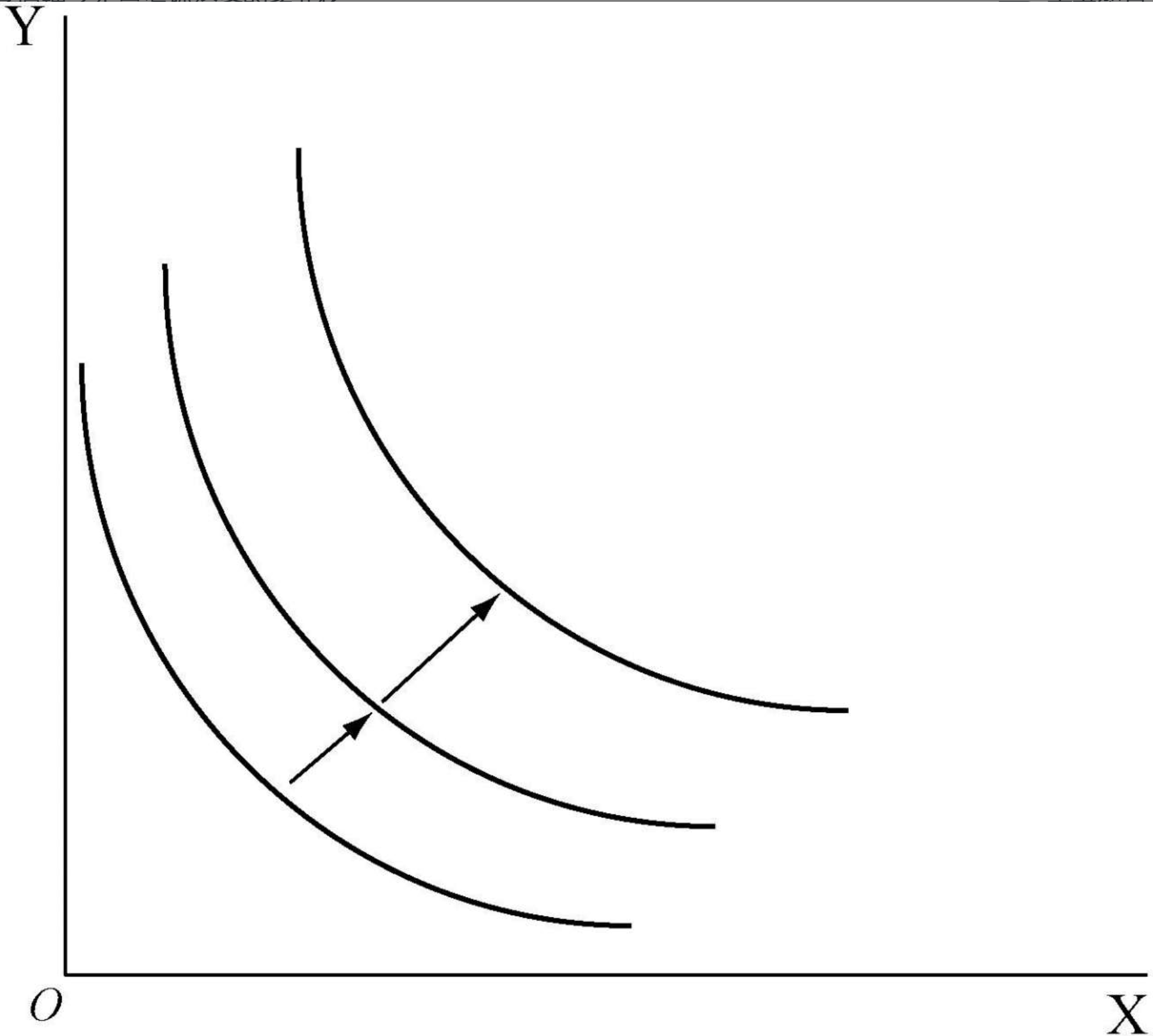
越往右上方的无差异曲线效用越高,越被偏好
劳动的边际效用为负,收入的边际效用为正
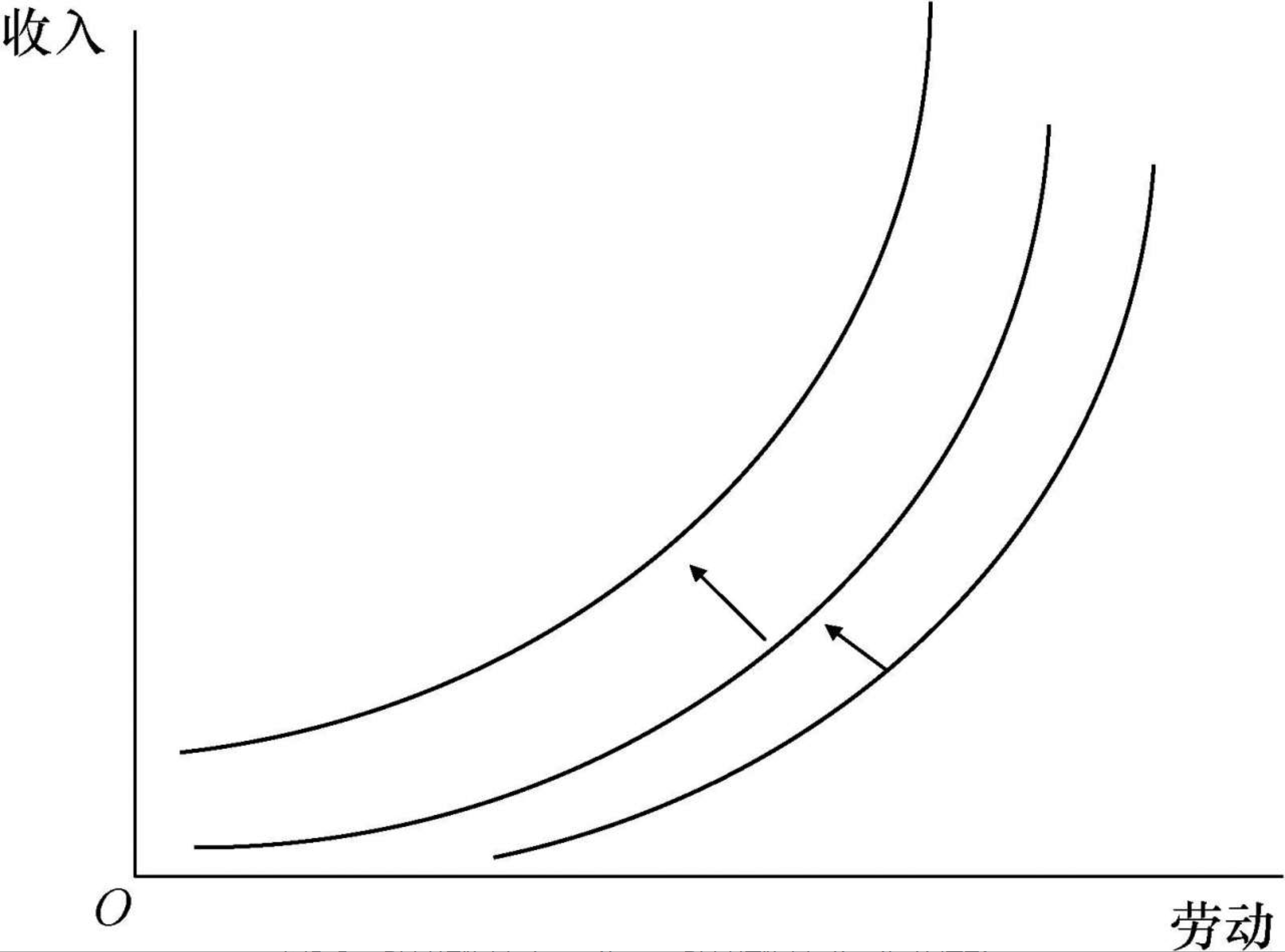
一种极端的无差异曲线——极乐点
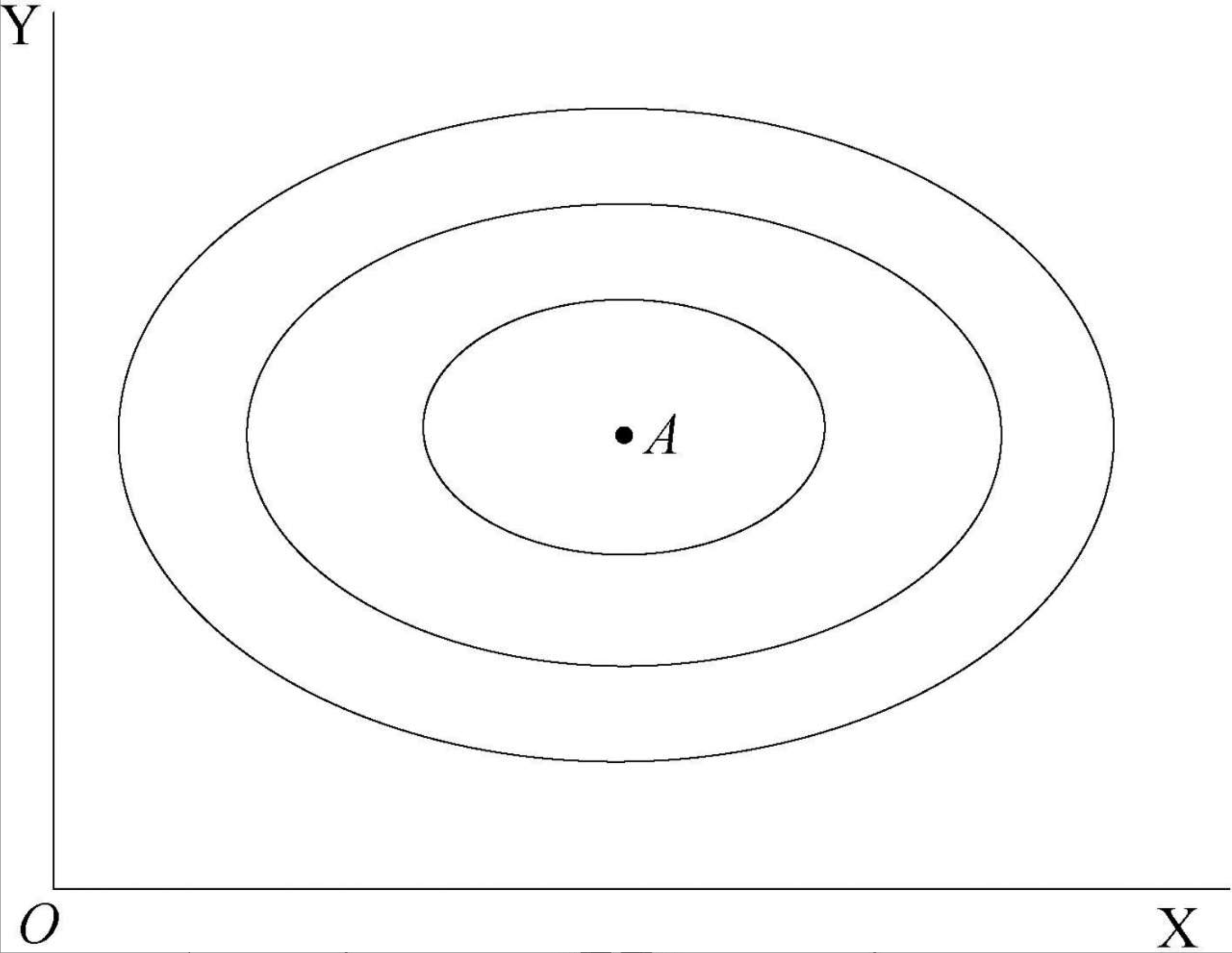
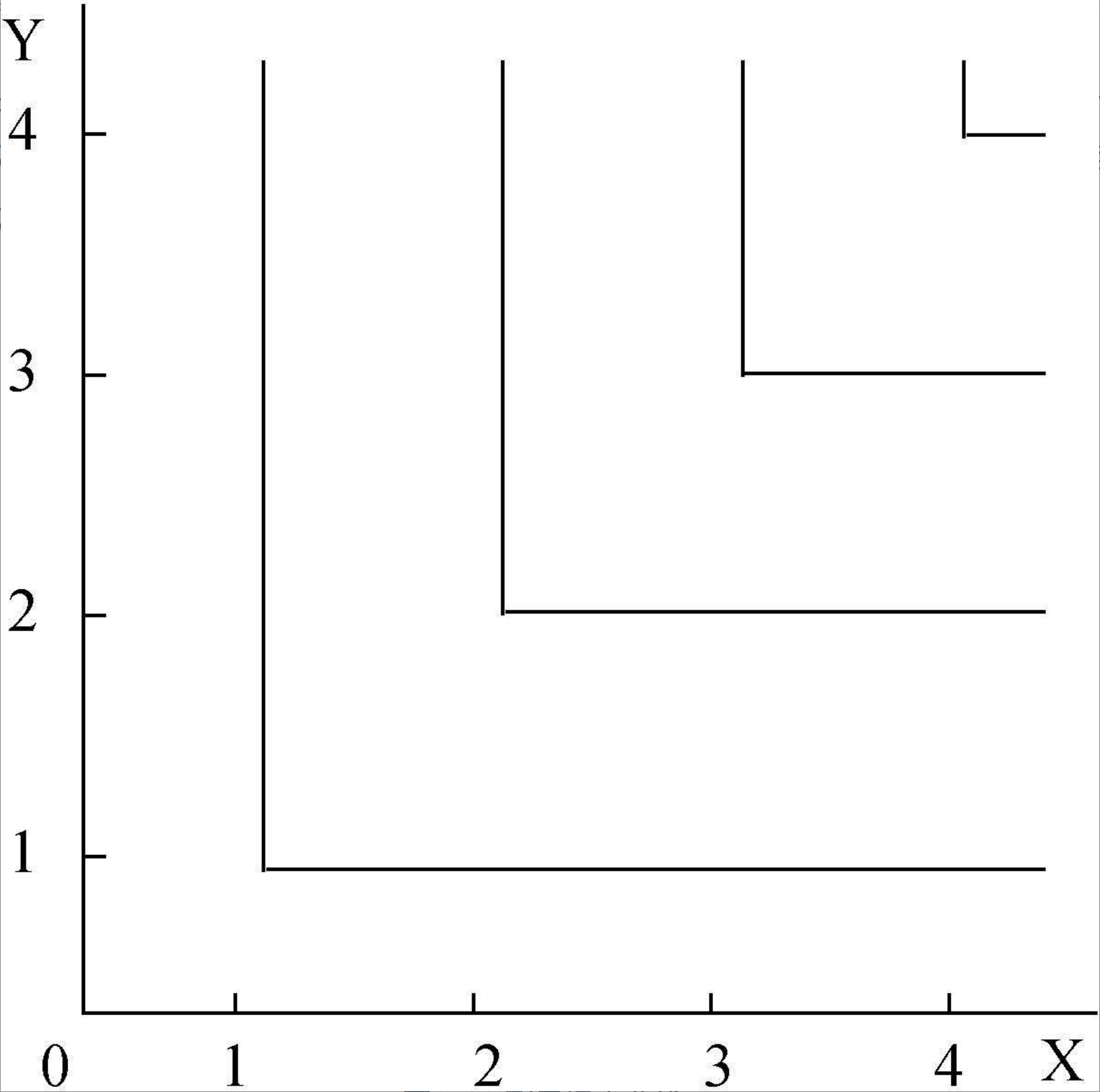
列昂惕夫无差异曲线
两种商品是绝对互补的:给定一个固定比例,除非两种商品同时增加,否则,再增加其中任何一种商品的数量都不会增加效用水平
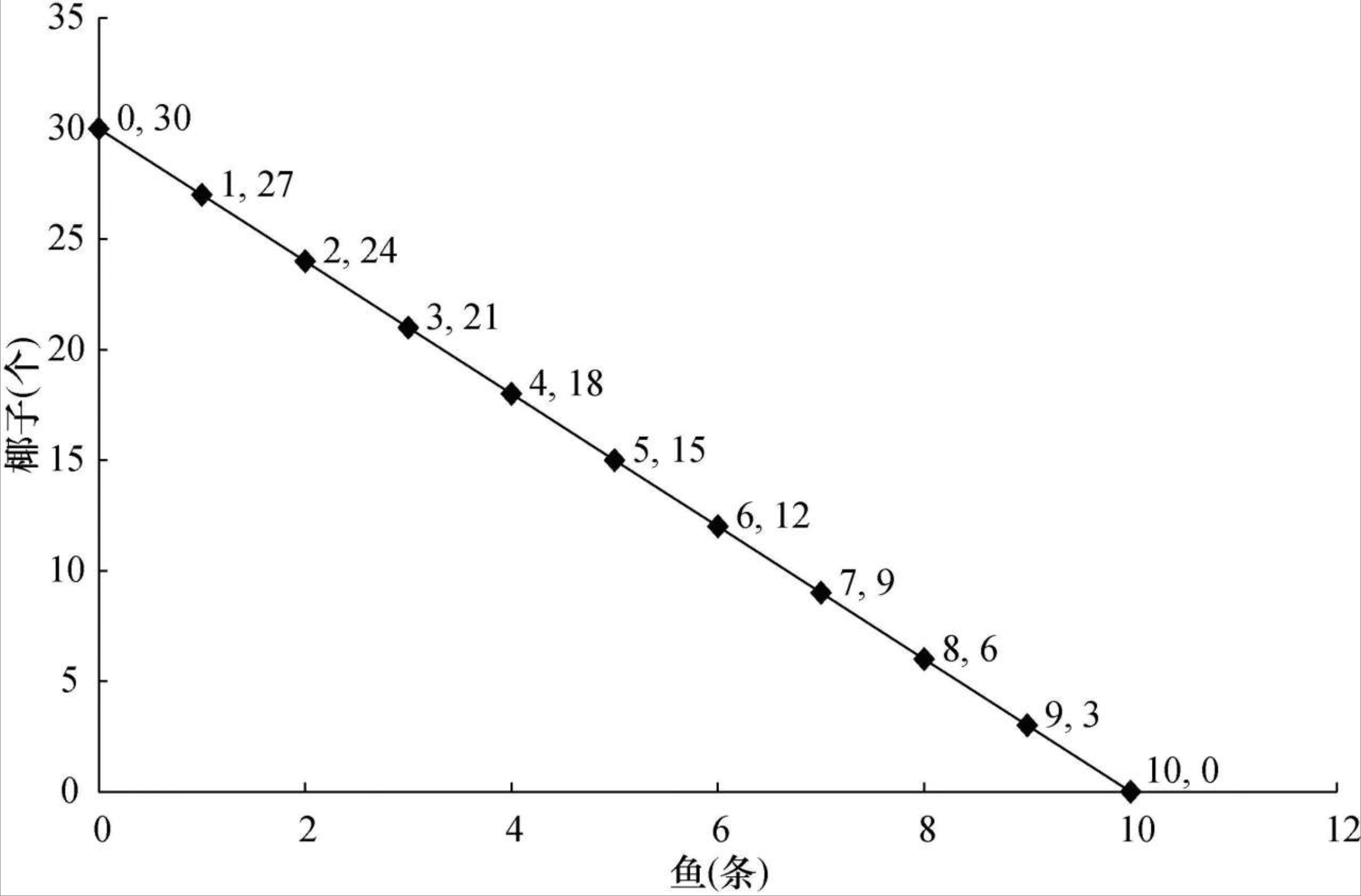
2.4.2 生产可行性曲线
机会成本:为了某个特定的行动而放弃的其他行动的最大收益。
生产可行性边界:给定资源和技术情况下可能实现的最大生产组合的集合。反映个体或社会面临的约束。
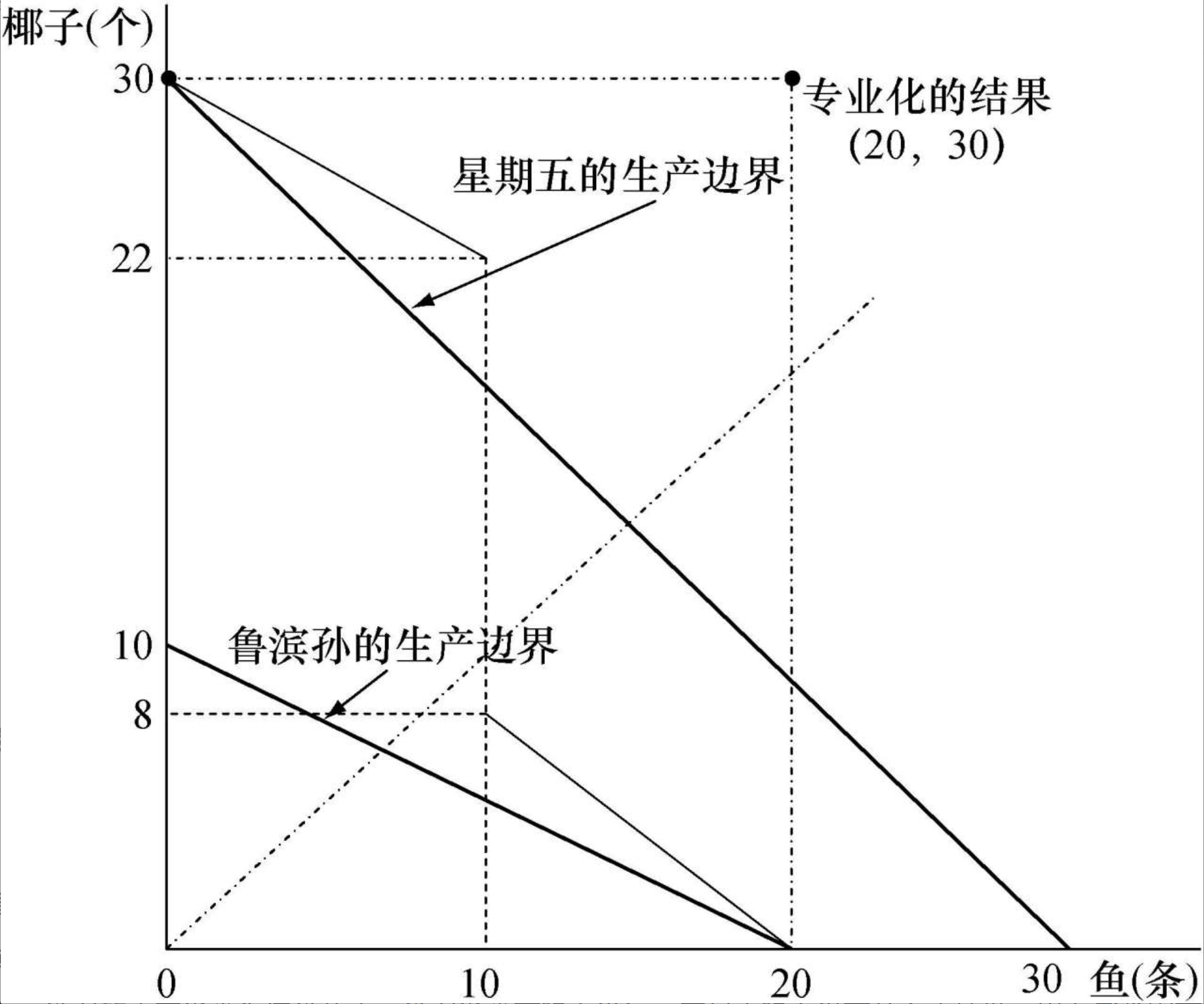
鲁滨孙的生产可行性边界
生产可行性边界的一般形式
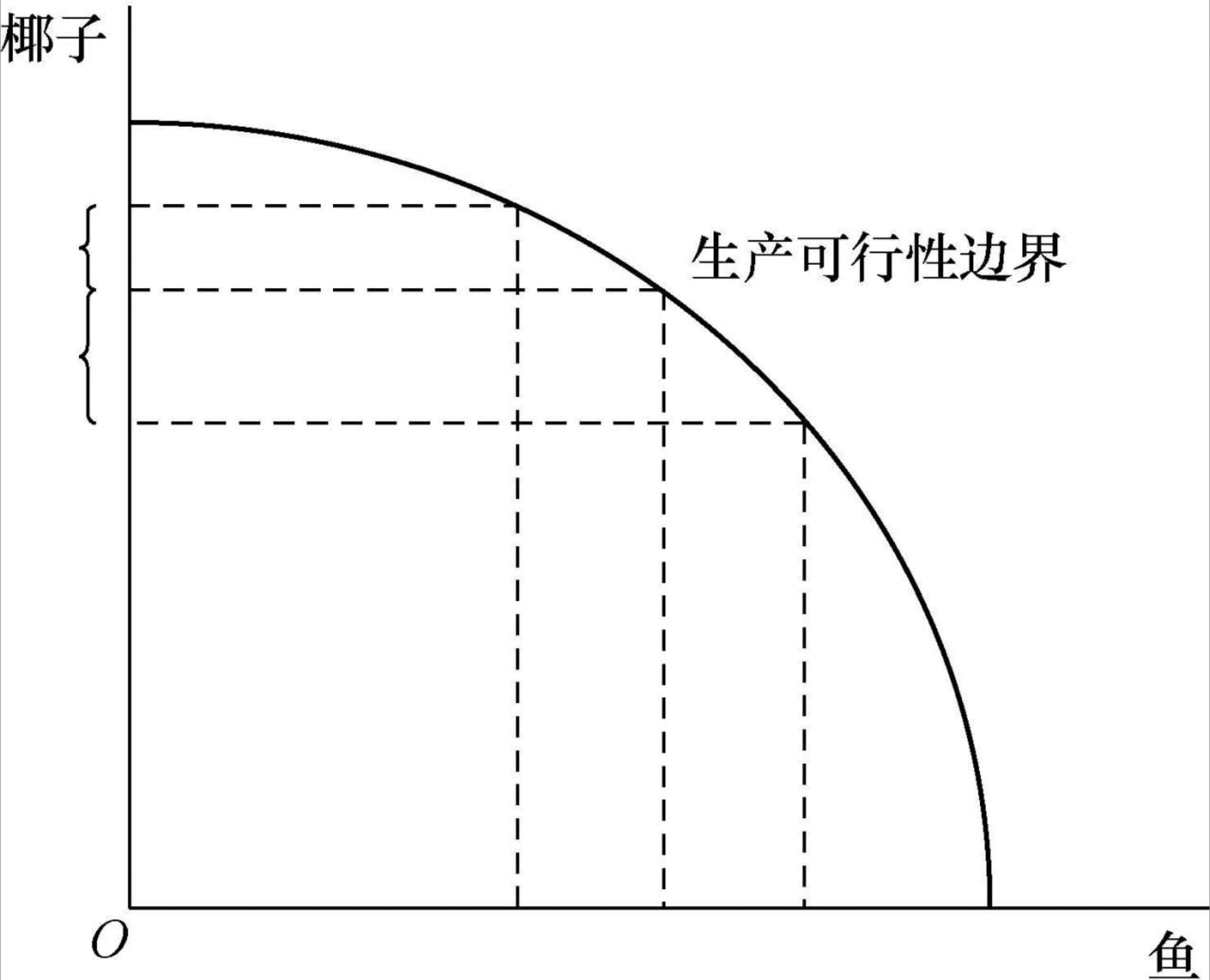
2.4.3 最优生产组合
最优选择条件:偏好上的边际替代率=生产上的边际转换率。
最优选择点:无差异曲线与生产可行性边界相切,这实际上是边际效用等于边际成本的另一种表达。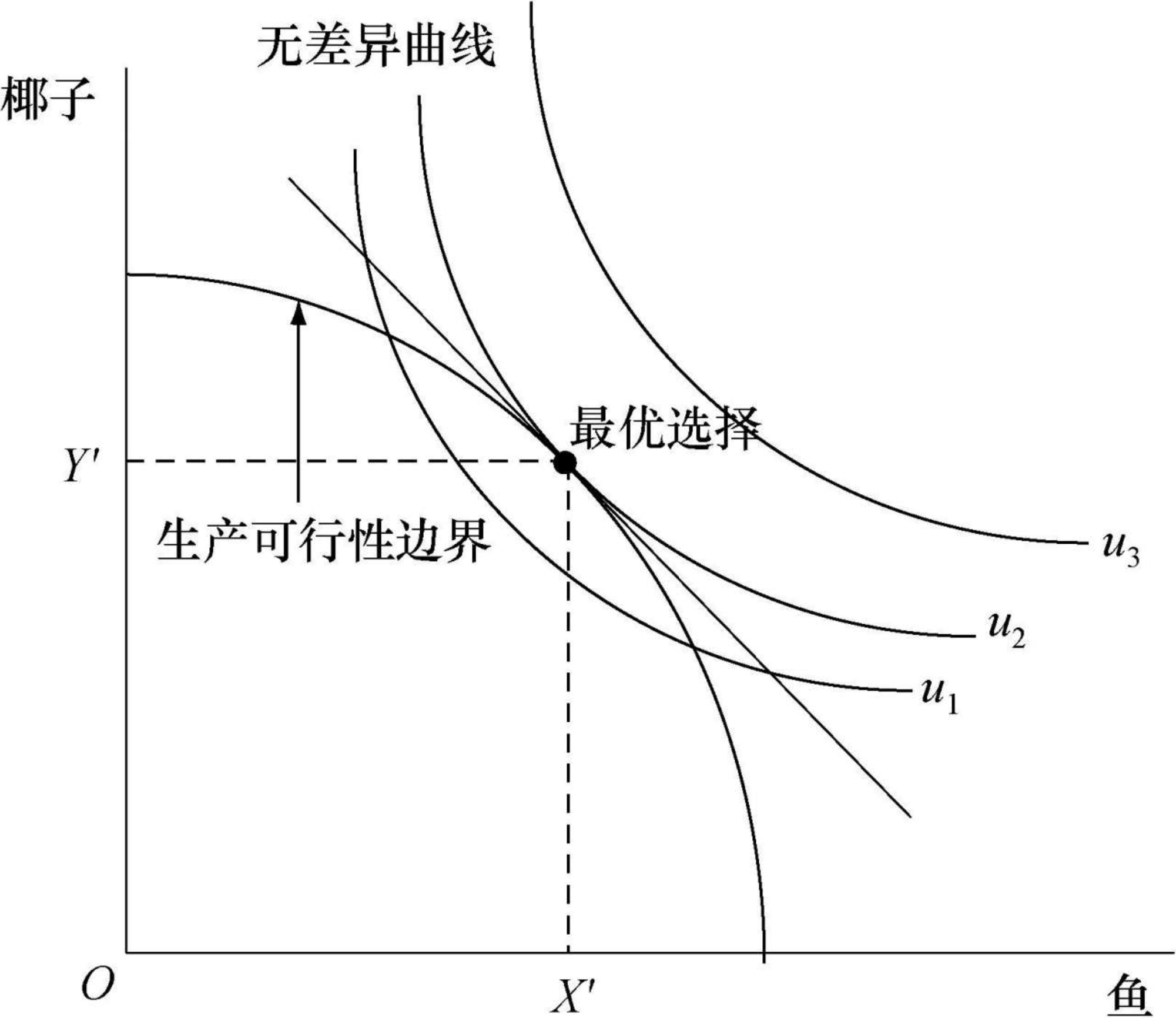
边际替代率:两种产品无差异曲线的斜率
边际转换率(即边际机会成本):两种产品在生产上的生产可行性边界斜率
2.4.4 经济扩展
通过减少短期消费而进行的储蓄和投资,可以增加资本品和改进生产技术,从而推动生产可行性边界向外移动。经济增长表现为由投资和生产技术改进带来的消费水平的不断提高。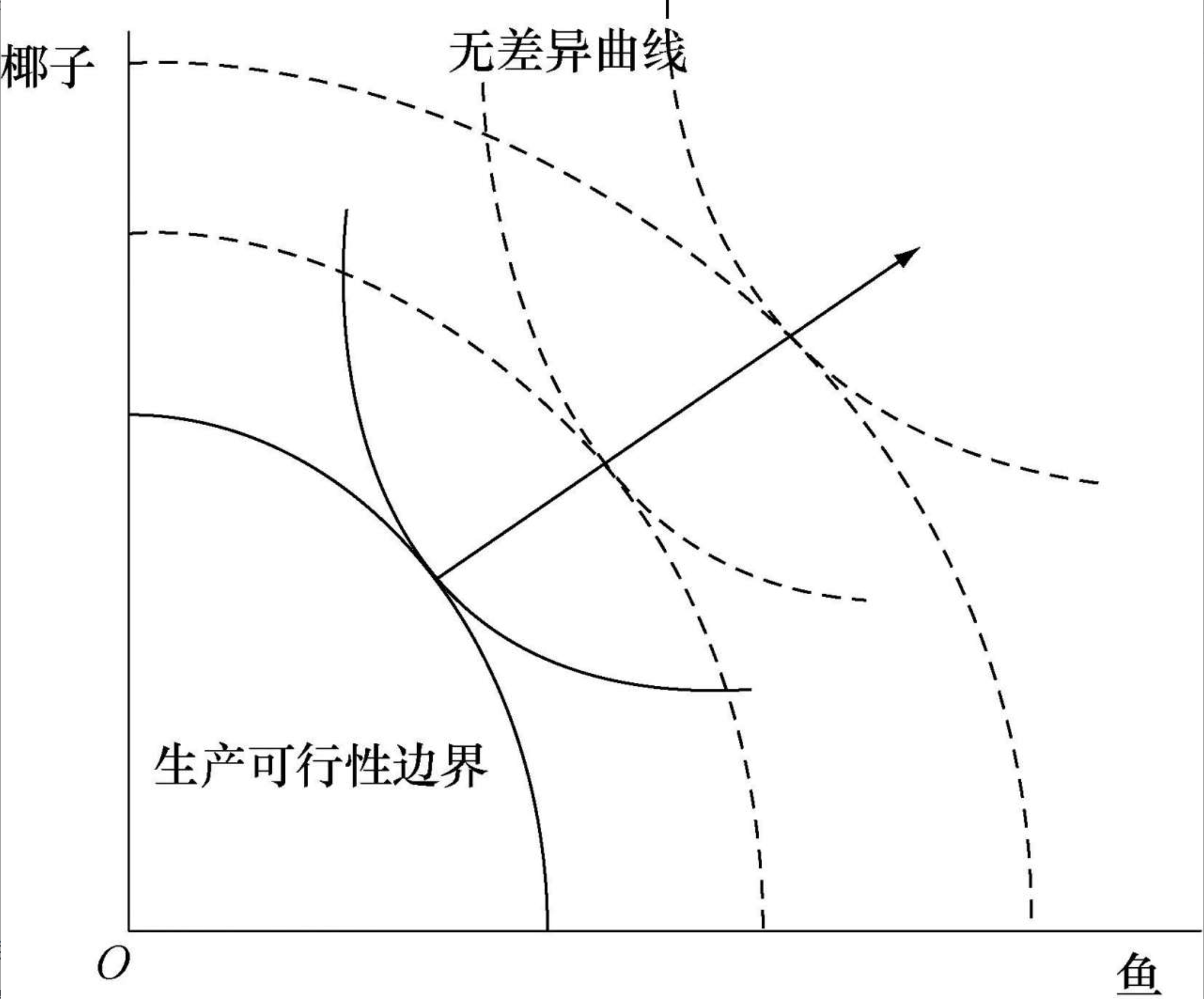
第3章 交换、分工与货币
交换:人们在自愿的基础上进行产品所有权转让以及其他形式的相互合作。
3.1 直接交换
直接交换:不借助于货币的物物交换,即以物易物。
价格:产品之间交换的比例,即某物品用另一种物品衡量的相对数字。
3.1.1 交换的好处
在只有两个人的交换中,能保证双方受益的交易价格不是唯一的;尽管交易使双方受益,但受益的程度会随交易价格的不同而不同。
实际的交易价格依赖于各自讨价还价能力。
如果参与交易的人数增加,交易价格的可行范围将不断缩小,自由竞争会使交易条件变得更为公平。
3.1.2 交换的无差异曲线分析
- 埃奇沃思盒状图

- 盒中的任意一点,对应的是两种产品在两个人之间的可行分配
- 由于两种产品都是好的物品,对每个人来说都是多多益善,因此,离各自坐标原点越远的无差异曲线效用水平越高。
均衡点:取决于双方讨价还价和偏好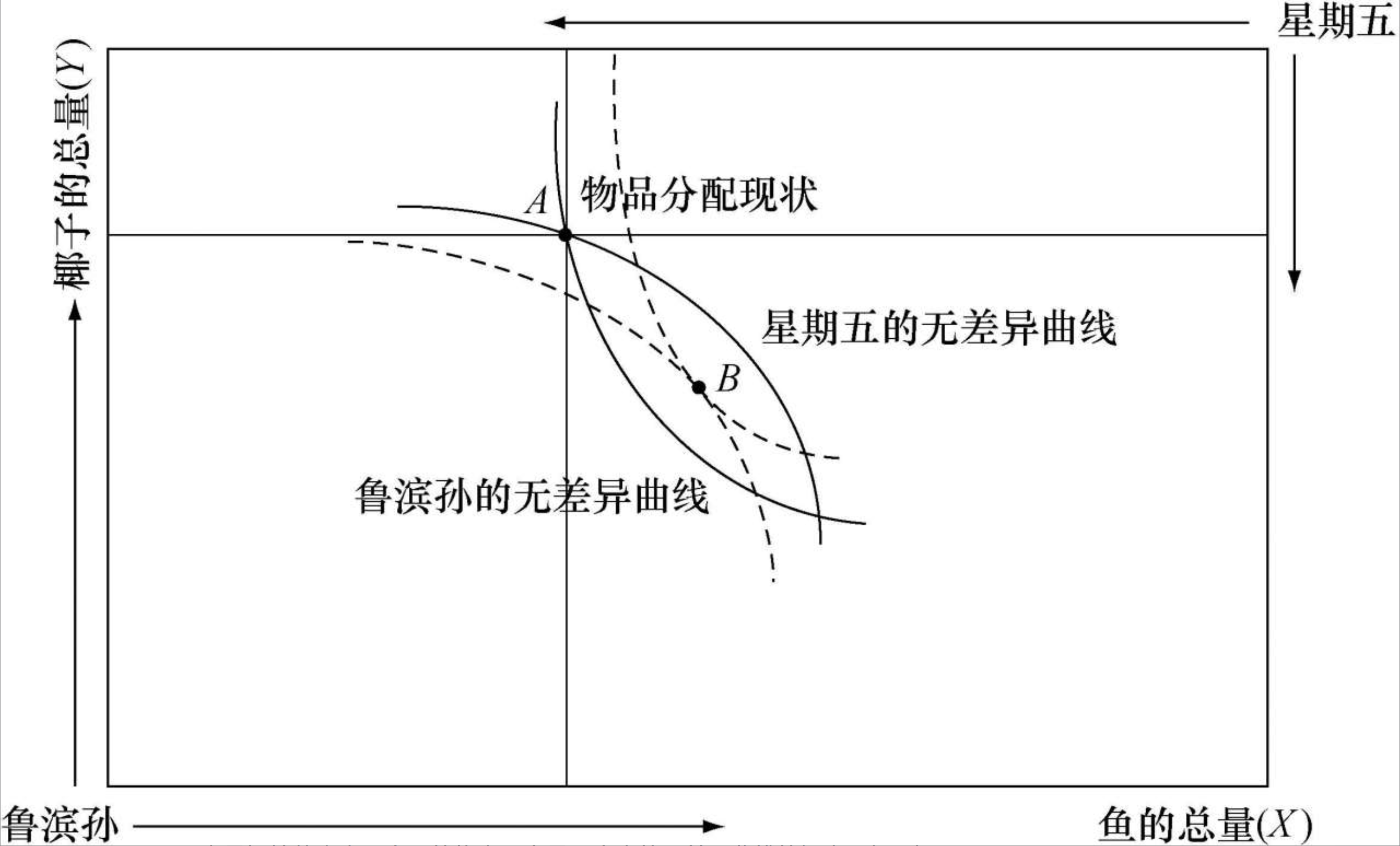
A点是初始状态点。交易的终点一定是两个人的无差异曲线的切点,如B点。
契约曲线:所有无差异曲线的切点构成的轨迹。
3.2 分工和比较优势
分工:不同的人专业化生产不同产品。
3.2.1 绝对优势和比较优势
绝对优势:一个人(国家)的某种产品的绝对生产率大于其他人(国家)
- 绝对优势导致的分工和变换
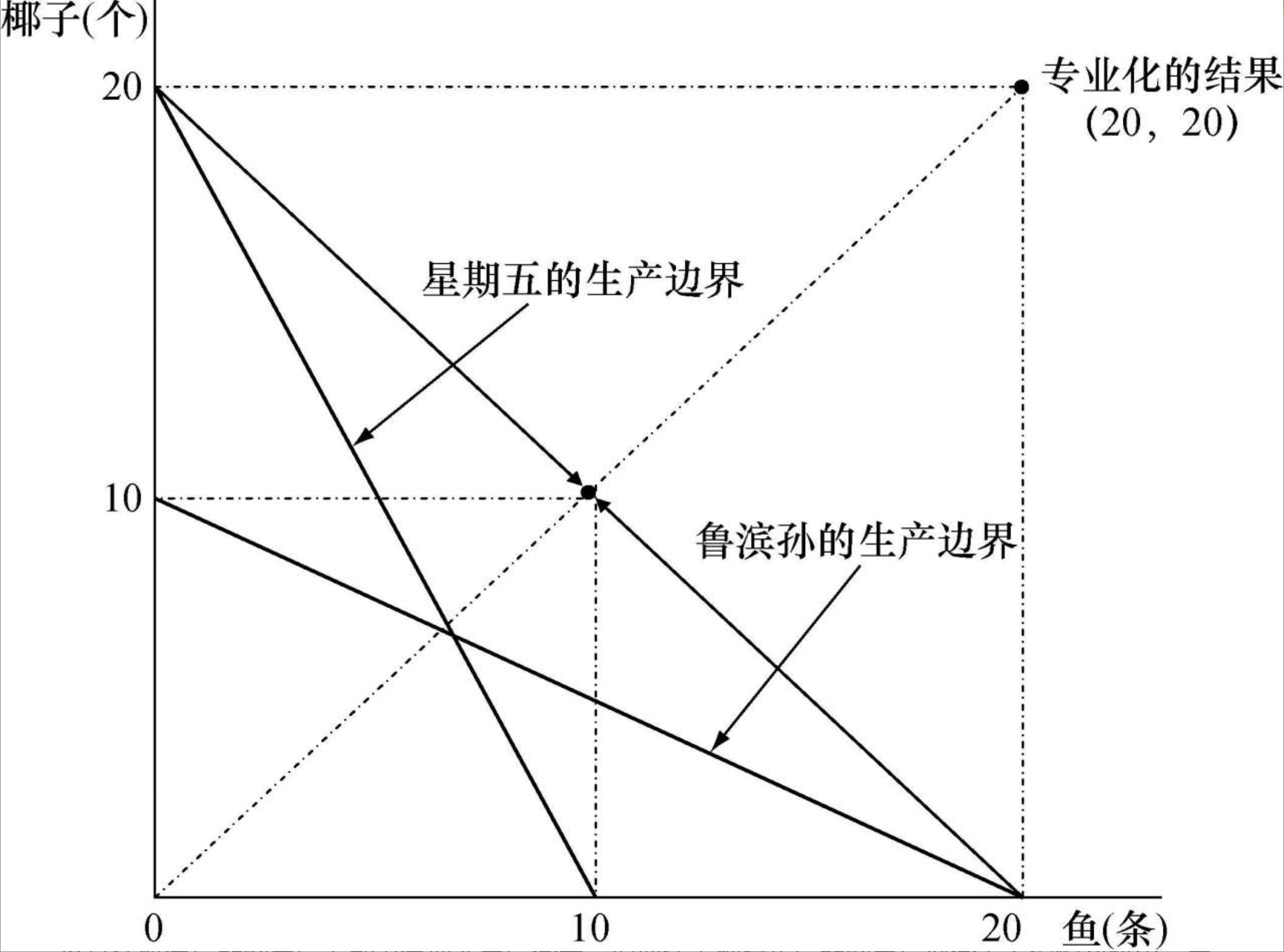
比较优势:一个人(国家)尽管在所有产品的生产上都没有他人生产率高,但在某种特定产品的生产效率上劣势相对较小,或者说,机会成本较小
- 比较优势导致的分工和变换
3.2.2 比较优势与国际贸易
如果每个国家专业化于自己具有比较优势的产品的生产,国际贸易可以给所有国家带来好处。
即便一国最初在任何方面都没有比较优势,但只要它专业化于某一特定的产业,日积月累,就可以在这个产业上形成自己的比较优势
根据比较优势原理,即使一国在所有商品生产上较之另一国均处于绝对劣势,但只要处于劣势的国家在各种商品生产上劣势的程度不同,也可以在劣势较小的商品生产方面具有比较优势,而处于优势的国家则在优势较大的商品生产方面具有比较优势。如果每个国家专业化生产和出口其具有比较优势的商品,进口其处于比较劣势的商品,则两国都能从贸易中得到利益,共同提升本国福利水平。——大卫·李嘉图1817年《政治经济学及赋税原理》
3.2.3 垂直分工
垂直分工:从原材料到最终产品生产过程中不同生产环节的分工。不同的生产者专业化于特定阶段产品的生产,每一个上游产品都作为下游产品的投入,直到最终生产出消费者需要的产品。
3.3 间接交换与货币
间接交换:以货币为媒介的交换。
3.3.1 货币的出现
货币:被广泛接受的交换媒介,能与任何商品交换,是所有产品的价格尺度。
交易成本:为了完成交易而必须支付的成本,包括寻找交易对象、谈判价格、签订合同、执行合同等过程中支付的成本等。
3.3.2 货币的演化
贵金属具有充当货币的最佳特征:
(1)单位价值高
(2)耐用,不易磨损
(3)运输方便
(4)质地均匀,易分割
(5)容易识别,不易伪造
纸币的信用来自政府的信用:纸币的生产成本很低,如果政府多印纸币,就可以把民间的财富转移到政府手里。如果纸币发行过滥,就会引起恶性通货膨胀,政府就失去了信用,人们就会寻求其他交易媒。
电子货币:某国的人民不相信政府,寻求另一种替代纸币的货币。
3.4 市场经济
3.4.1 生产者和消费者的分离
简单的产品交换:长期的农业社会,人们生产产品主要是为了自己消费,生产者和消费者是一体的,交换只是互通有无、调剂余缺。
产品变成了“商品”:随着交换和分工的发展,出现了“市场经济”,生产和消费分离,生产者生产的产品主要不是为了自己消费,而是为了在市场上出售;消费者消费的产品通常也不是自己生产出来的,而是要从市场上购买。
分离导致的竞争:生产者之间要为出售商品而竞争,消费者之间要为购买商品而竞争
3.4.2 经济循环流模型
经济学家的两大类市场:第一类是产品市场,第二类是要素市场。
经济循环流模型:反映家庭和厂商之间在产品市场和要素市场上的支出和收入关系的模型。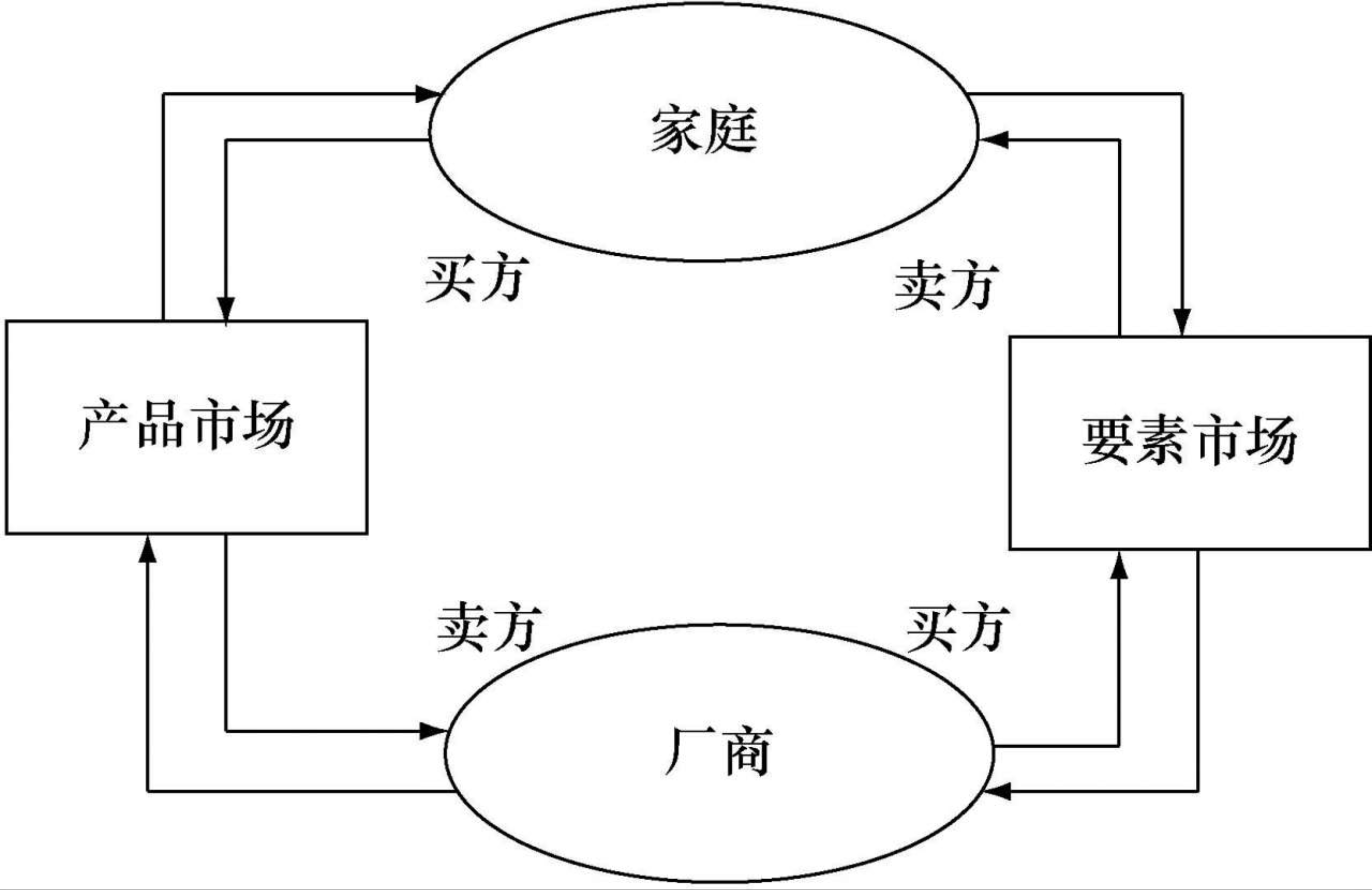
凯恩斯主义经济学的总量分析之所以有问题,一个重要的原因是它忽略了中间产品的交易。
3.4.3 价格的功能
价格是在竞争中形成的,不是由任何单一的权威机构规定的。价格不仅决定生产什么和如何生产,而且决定收入分配(为谁生产)。
价格机制自发地协调着生产和消费,被认为是人类最伟大的创造之一。在人类交易的过程中,再也找不到比价格机制更有效的协调方式。
价格的三个功能:
- 传递信息:需求增加则价格上涨,价格上涨导致需求降低。
- 提供激励:生产者根据产品和要素价格的变化调整产出和投入,以增加利润,激励生产者寻找替代品和开发新技术。
- 决定收入分配:价格之所以有激励功能,是因为它决定每个人的收入。
第4章 消费者选择与需求曲线
4.1 最优消费组合选择
4.1.1 无差异曲线(重复)
4.1.2 预算约束线
预算约束线:用于购买商品的总支出等于总收入。预算约束线上的所有消费组合都是可行的。
收入变动引起的预算约束线变动:如果收入M发生变化但价格不变,预算约束线会平移:M⬆️,线右移;M⬇️,线左移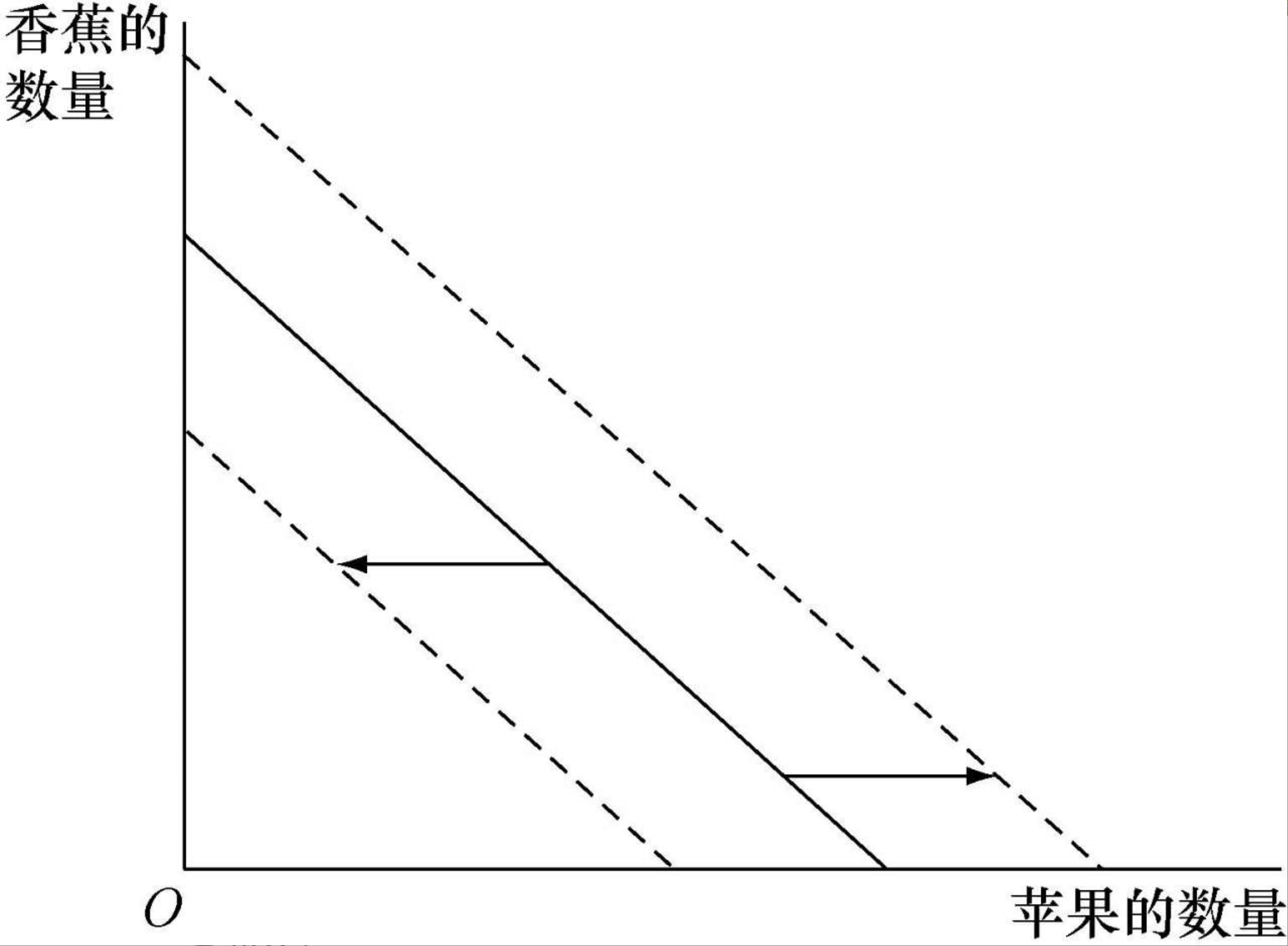
苹果价格单方面变动引起的预算约束线变动:某种商品的价格单方面变动时,预算约束线将发生旋转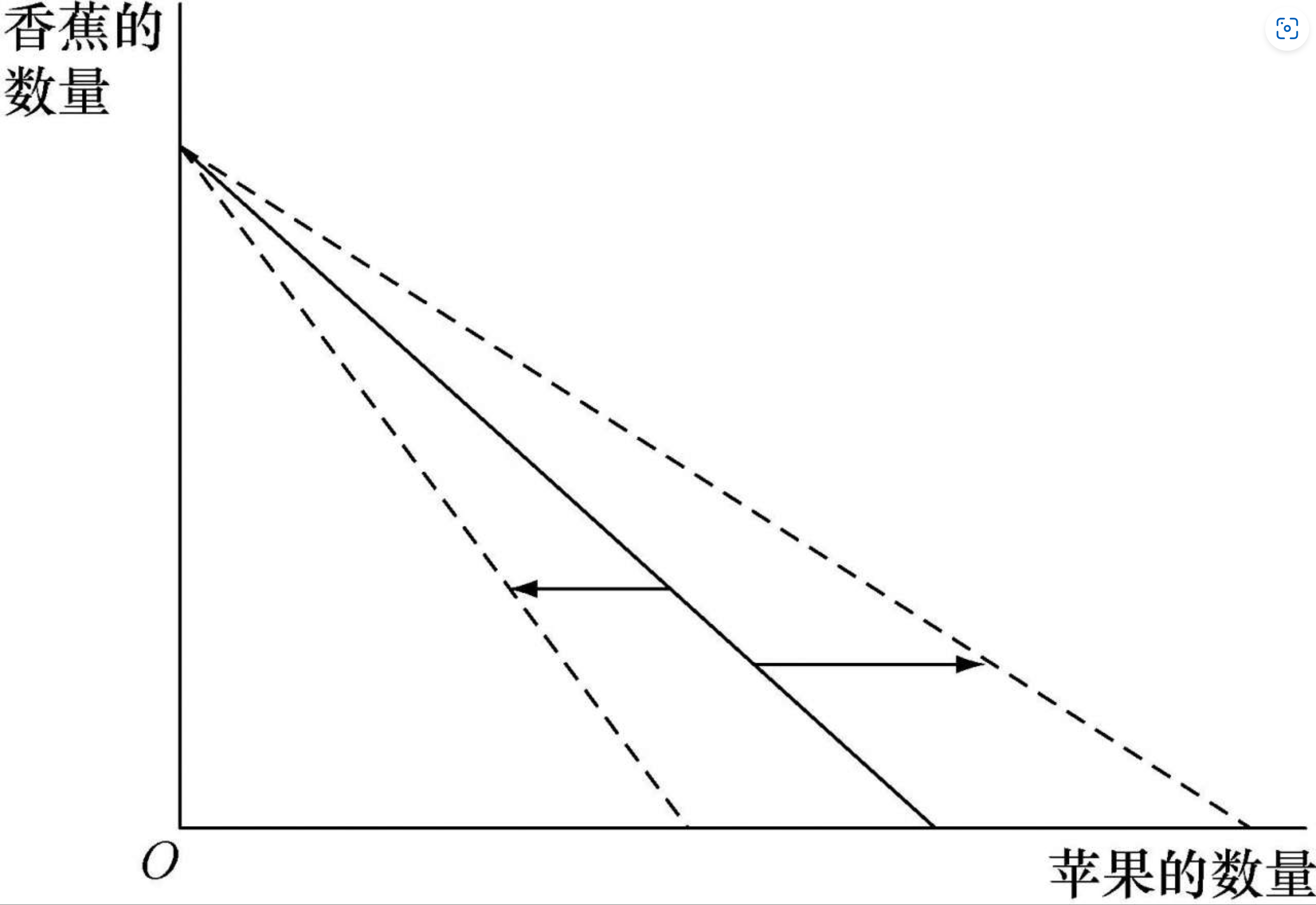
4.1.3 最优消费组合
给定消费者偏好、预算约束和价格,实现最大效用水平:图中有预算约束曲线,三条无差异曲线。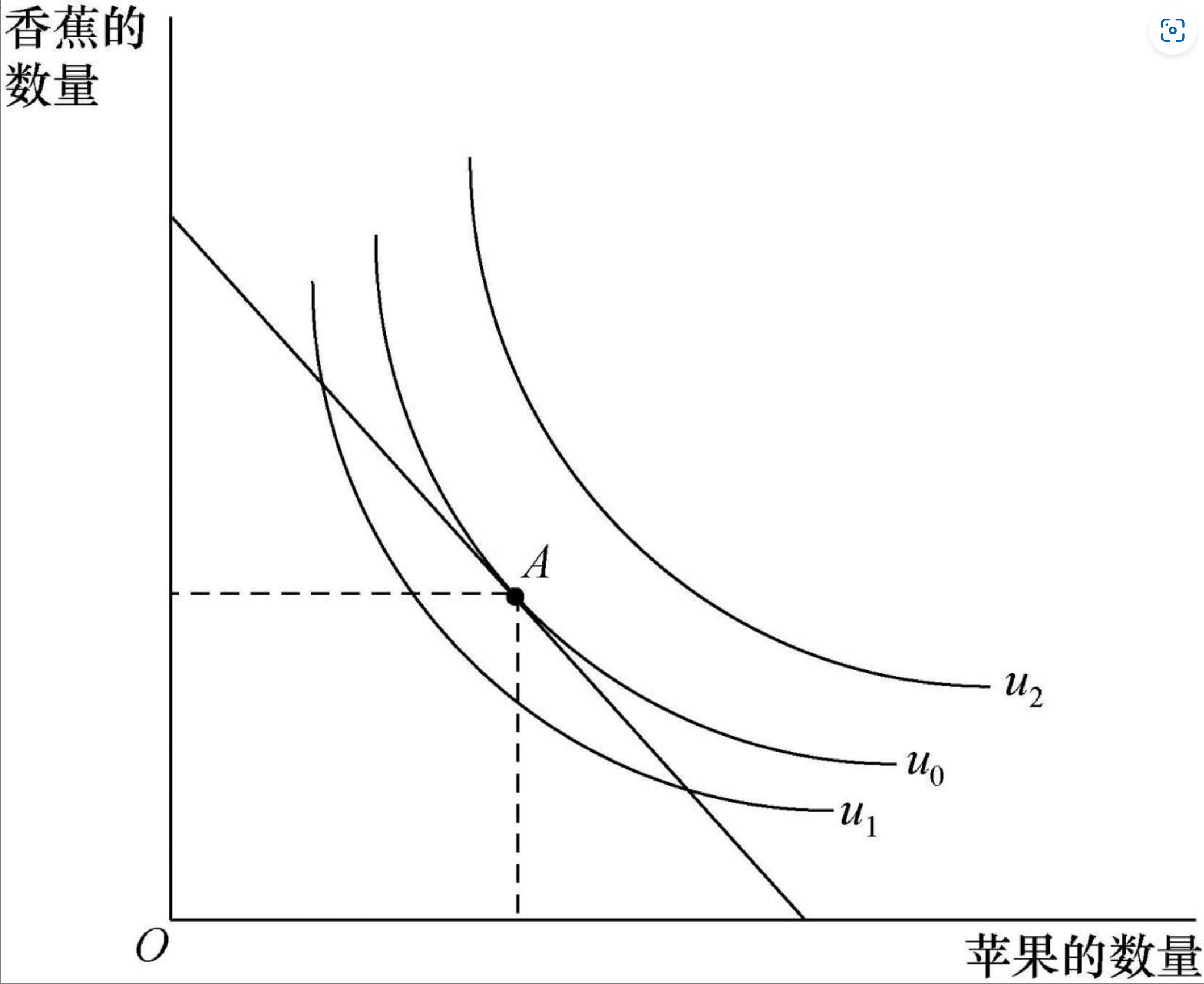
最优消费选择:无差异曲线与预算曲线相切
预算线的斜率的绝对值:两种商品的价格之比,$pa/pb$
无差异曲线的切线的斜率为边际替代率:$$MRS_{ab} = \frac{\Delta x_b}{\Delta x_a} =\frac{\partial u/\partial x_a}{\partial u/\partial x_b} \Longrightarrow \frac{\partial u/\partial x_a}{p_a}=\frac{\partial u/\partial x_b}{p_b} $$
最优消费选择的直观经济含义:最后1分钱无论用于哪种商品的消费,给消费者带来的满足程度是一样的。
若等式不成立,说明消费者可在相同预算下变换消费结构,降低单位边际效用低的商品消费,增加单位边际效用高的商品消费,从而让自己的福利进一步提高,说明当前状态就不是效用最大化状态了。
4.2 比较静态分析
需求函数:需求量与价格、收入的关系。
4.2.1 偏好变化
不同偏好对应的不同选择:新的偏好下,原来的最优选择就不再是最优的了,因为最后1分钱花在苹果上的边际效用小于花在香蕉上的边际效用,消费者会减少苹果的消费同时增加香蕉的消费,直到两种产品上的边际效用相等为止。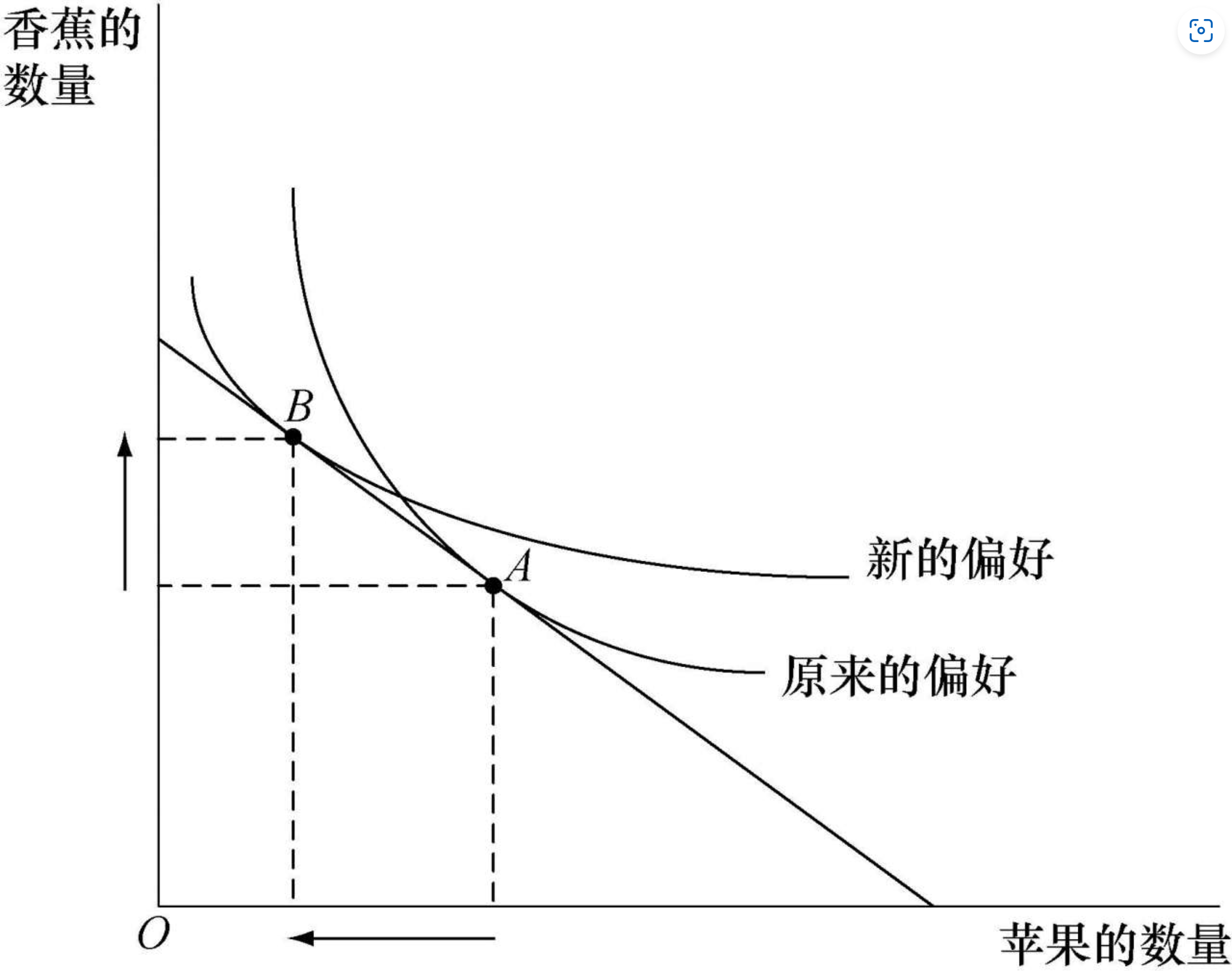
4.2.2 收入变化
收入增加对正常商品组合的影响: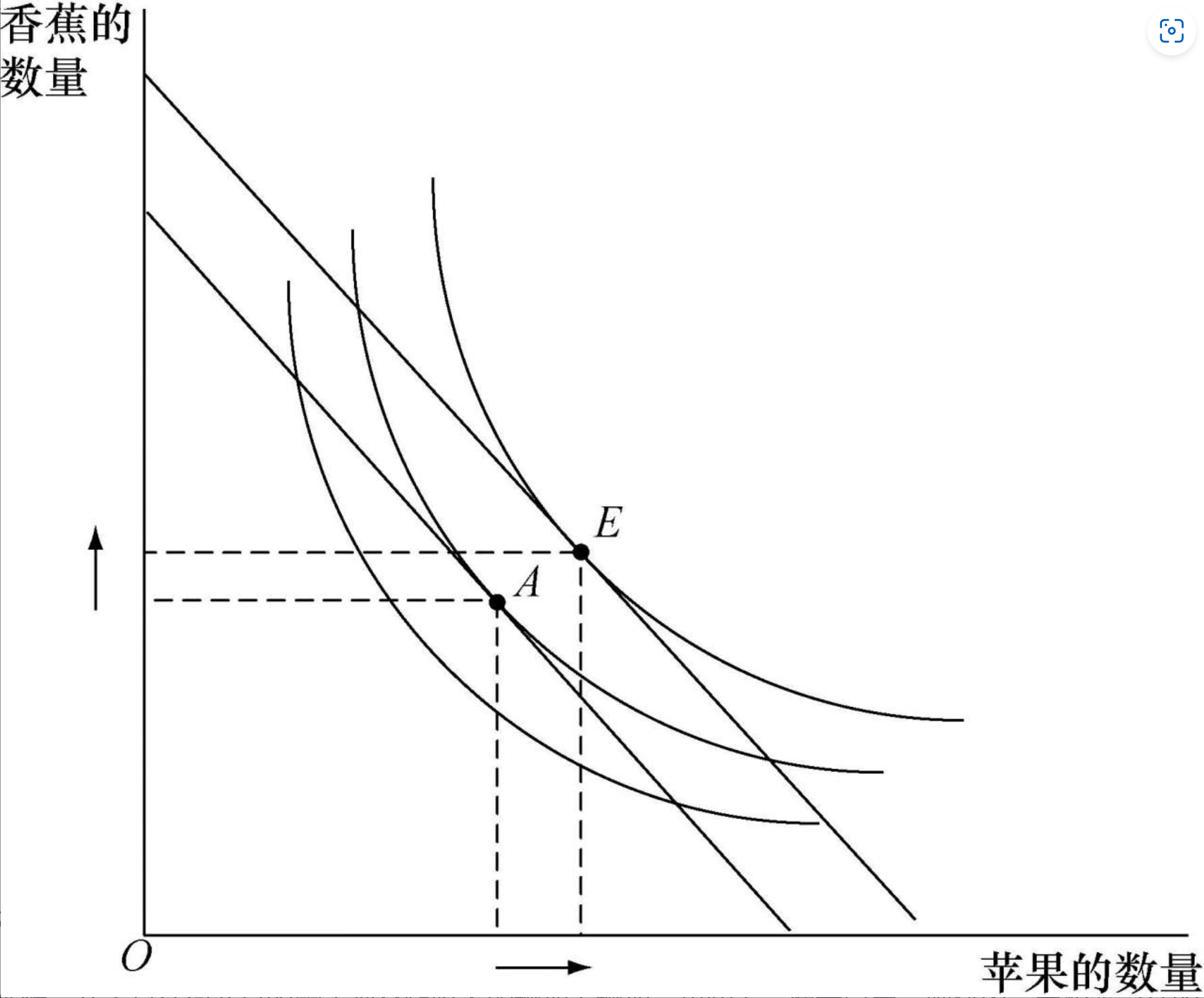
并不是任何商品的需求都会随收入的增加而增加。事实上,像大白菜、肥猪肉、面粉等这样的产品,随着人们的收入提高,对它们的消费反倒减少了。
正常商品(normal goods):消费数量随着收入增加而增加。
劣等商品(inferior goods):消费数量随着收入增加而下降。
一种商品是劣等品的最优消费组合情况: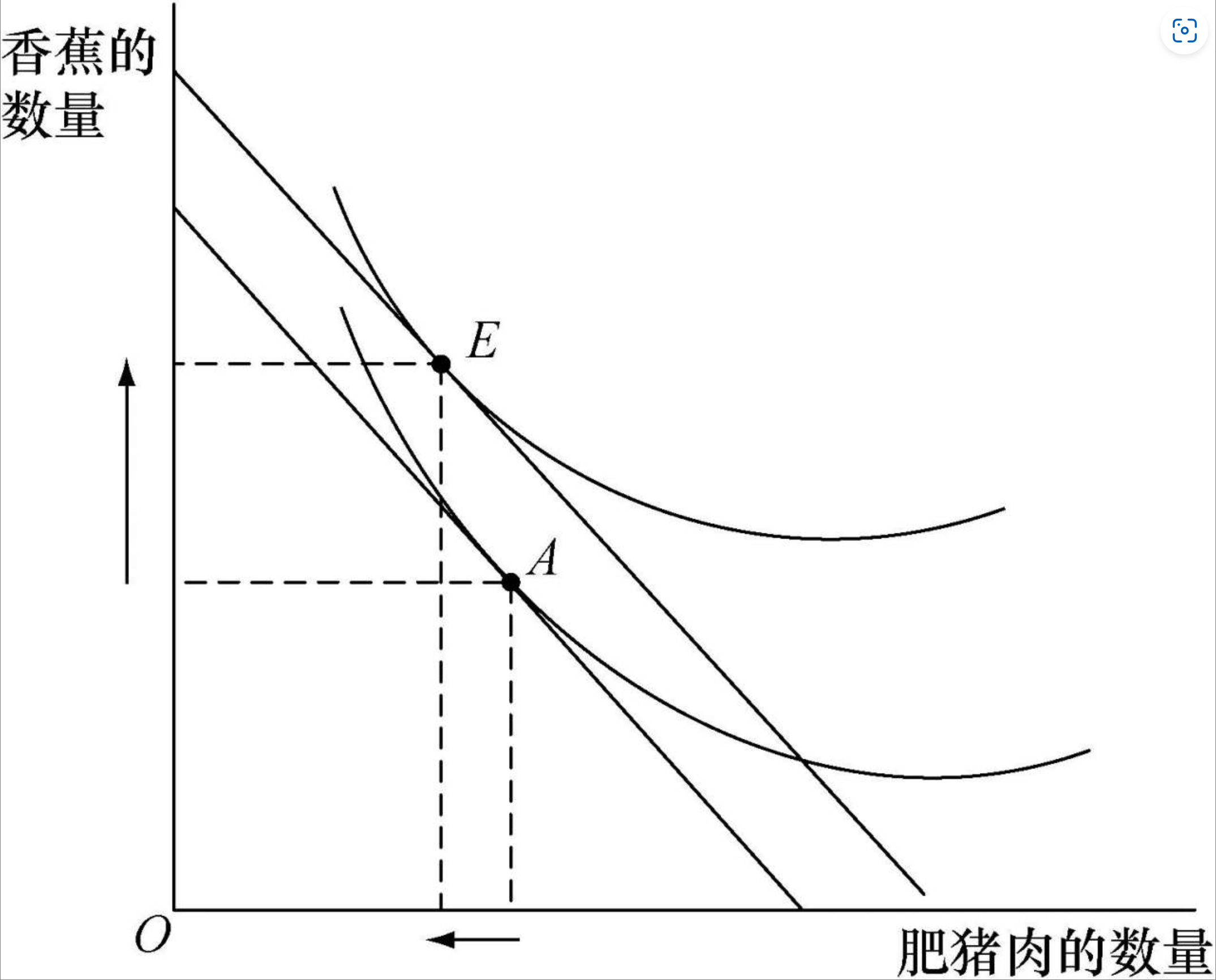
4.2.3 价格变化
苹果价格下降的最优消费组合情况: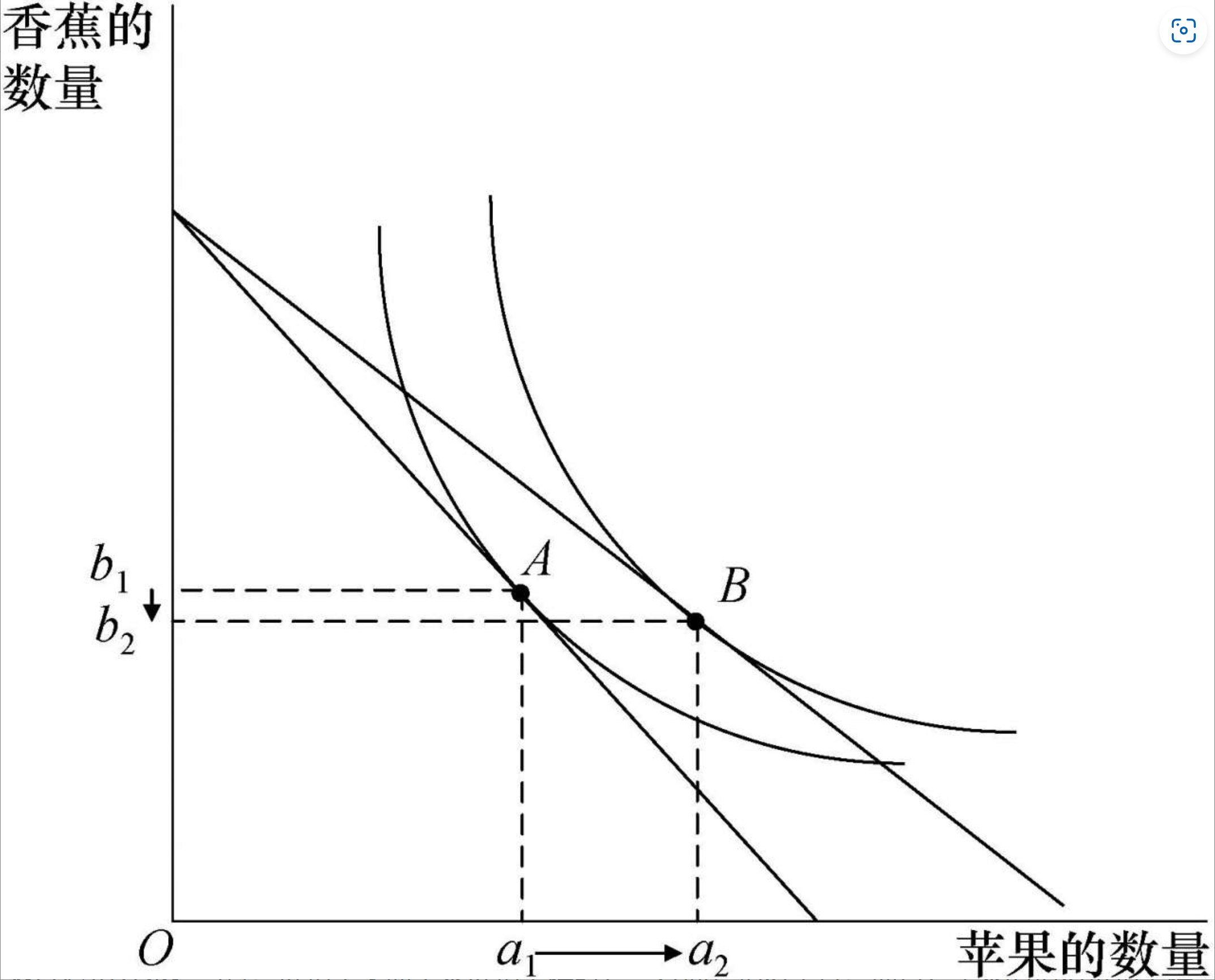
不是所有商品的需求都随自身价格的下降而增加的,商品和商品之间存在替代效应和收入效应。
替代效应:在真实收入不变的情况下,由相对价格变化引起的需求的变化。
收入效应:由于收入变化引起的需求的变化。
价格效应:由价格变化引起的收入效应和替代效应之和。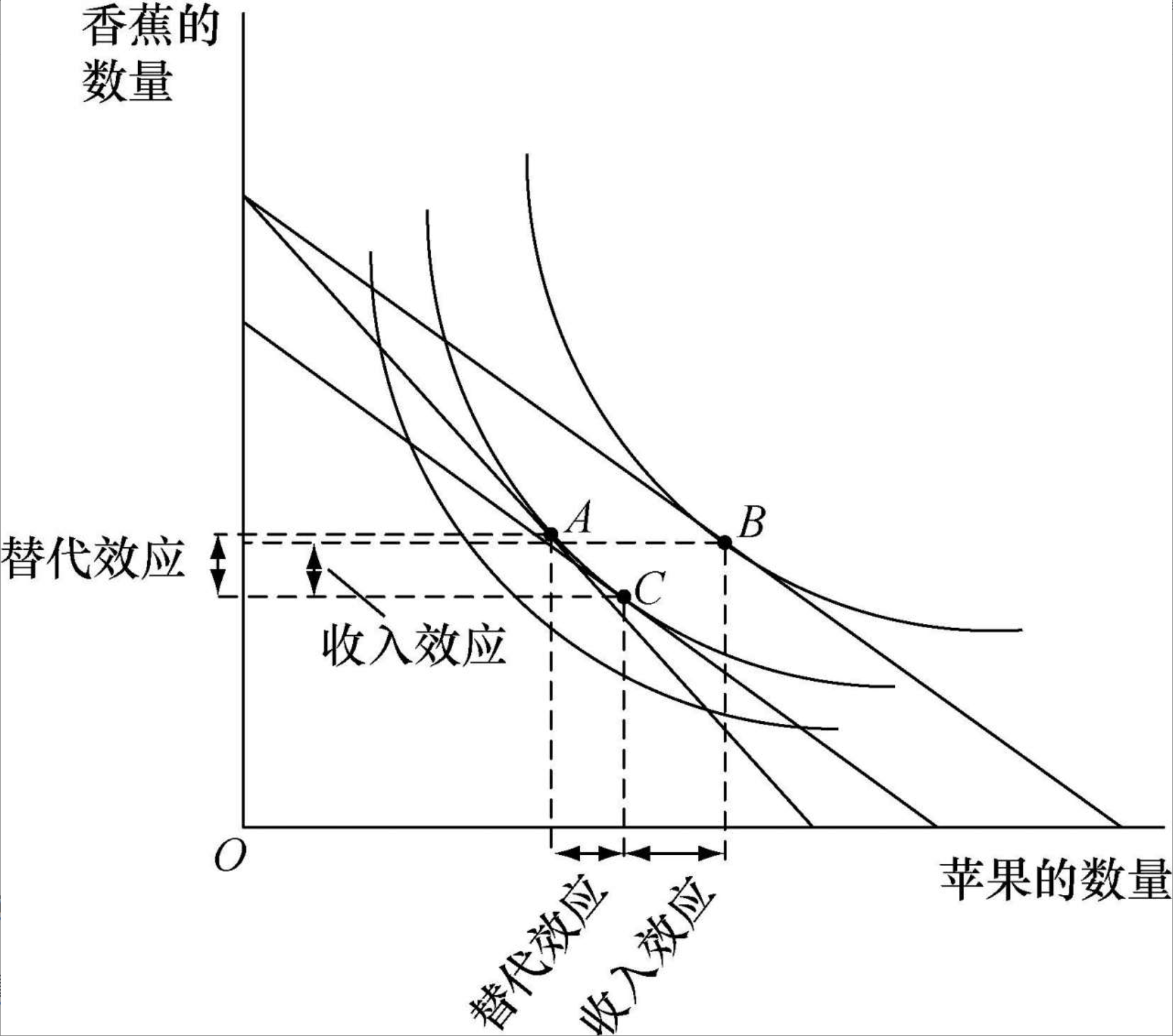
从A点到C点的变动是替代效应,从C点到B点的变动是收入效应。
吉芬商品(Giffen goods):需求随价格的下降而下降的商品。
4.2.4 间接效用函数
直接效用函数(direct utility function):消费者的偏好是直接定义在产品上的效用函数(给定收入和偏好)。
直接效用函数数学式:
$$ u(x1,x2,…,x_N)$$
间接效用函数(indirect utility function):效用函数定义在价格和收入水平上,再把需求函数代入直接效用函数,构造出一个复合效用函数。
间接效用函数数学式:
$$\begin{array}{c}
u(p1,p2,…,p_N,M)= \max u (x1,x2,…,x_N)\
s.t.\sum_{N}^{i=1}p_ix_i=M
\end{array} $$
4.3 个人需求曲线与需求法则
4.3.1 需求曲线
需求曲线:消费者对产品的需求量与该产品价格之间的关系。
苹果价格下降,最优消费组合变动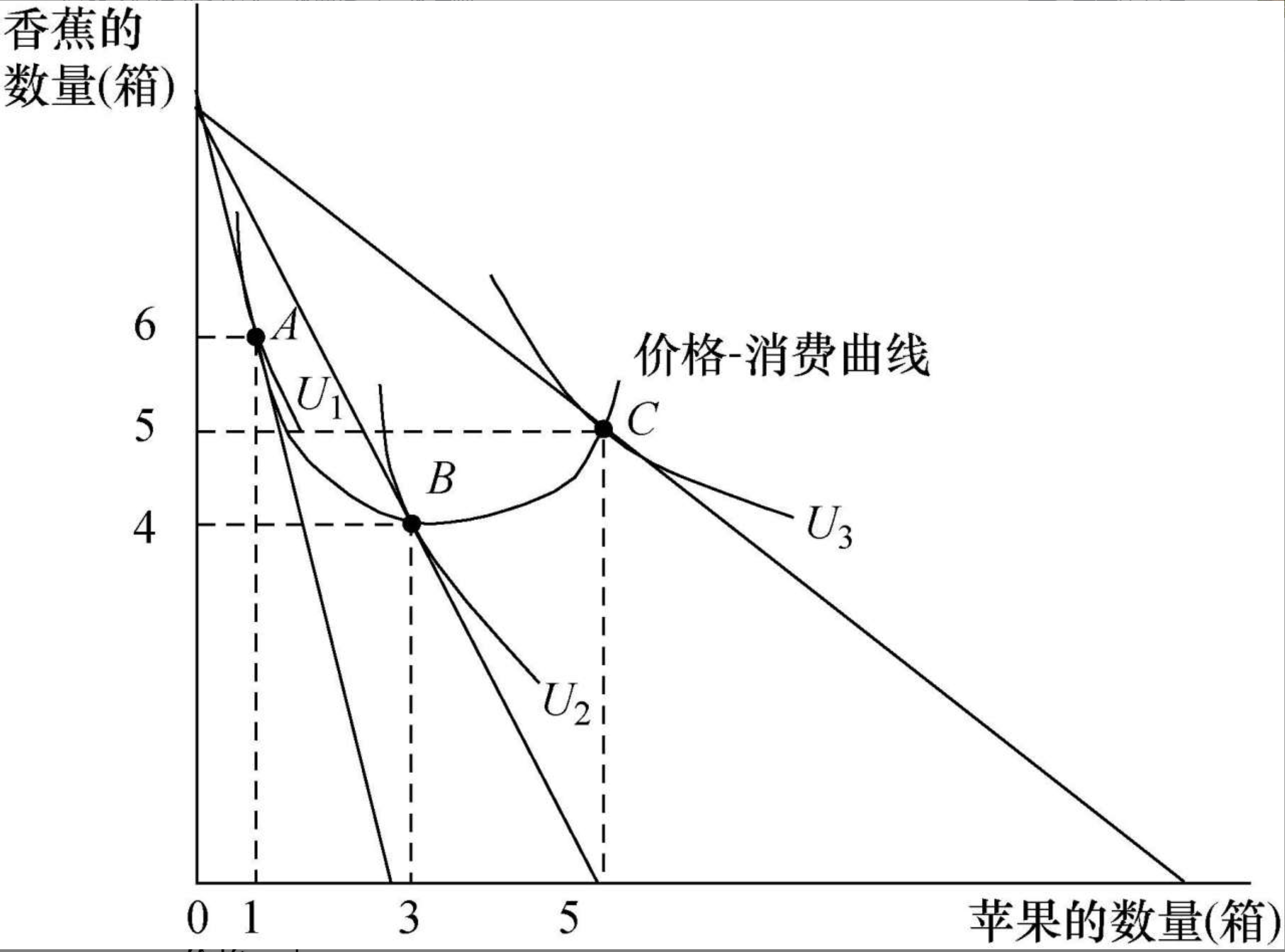
对应的苹果的需求曲线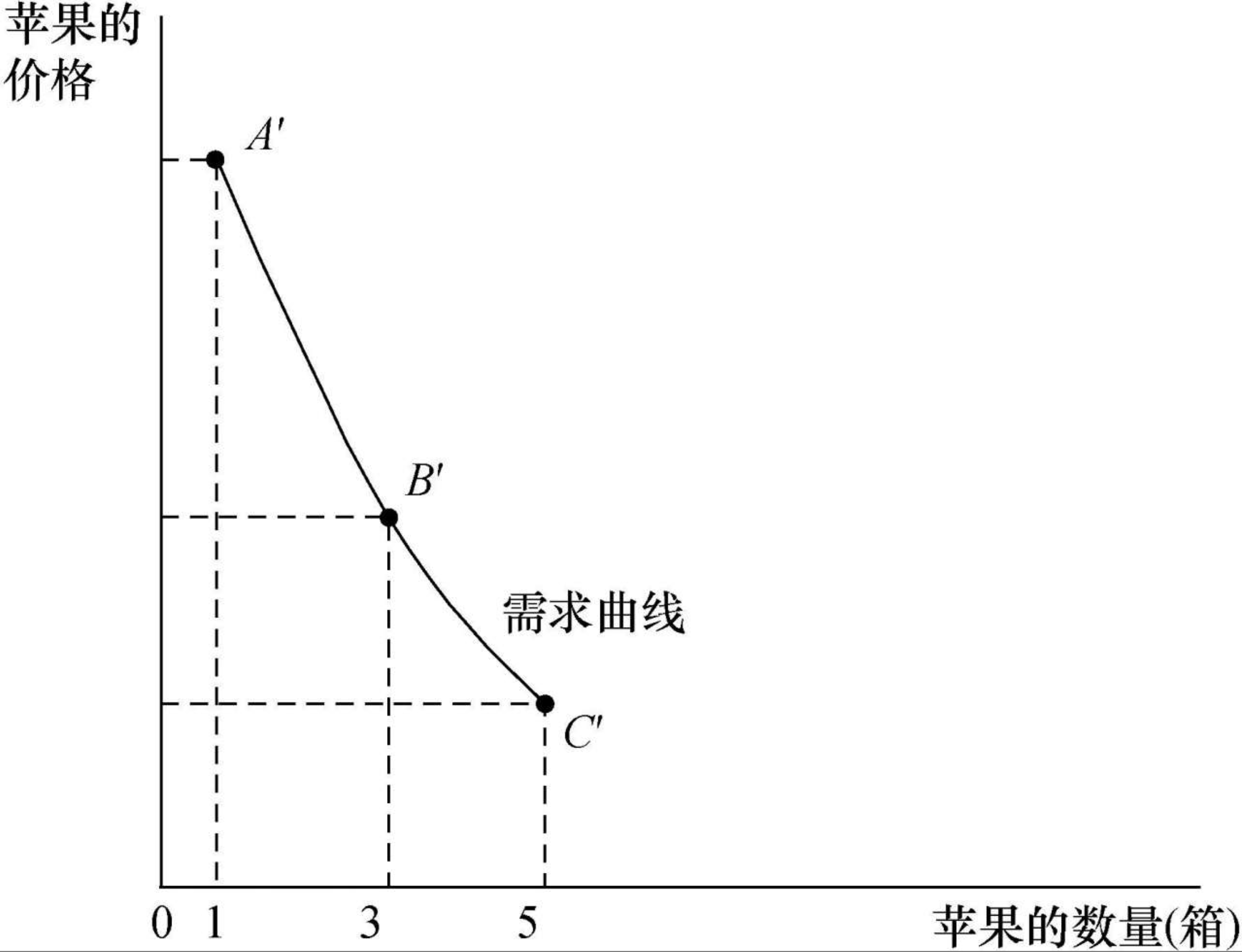
4.3.2 需求曲线的移动
替代品:一种商品价格上涨导致另一种商品的需求上升。
代品价格上升引起的需求曲线移动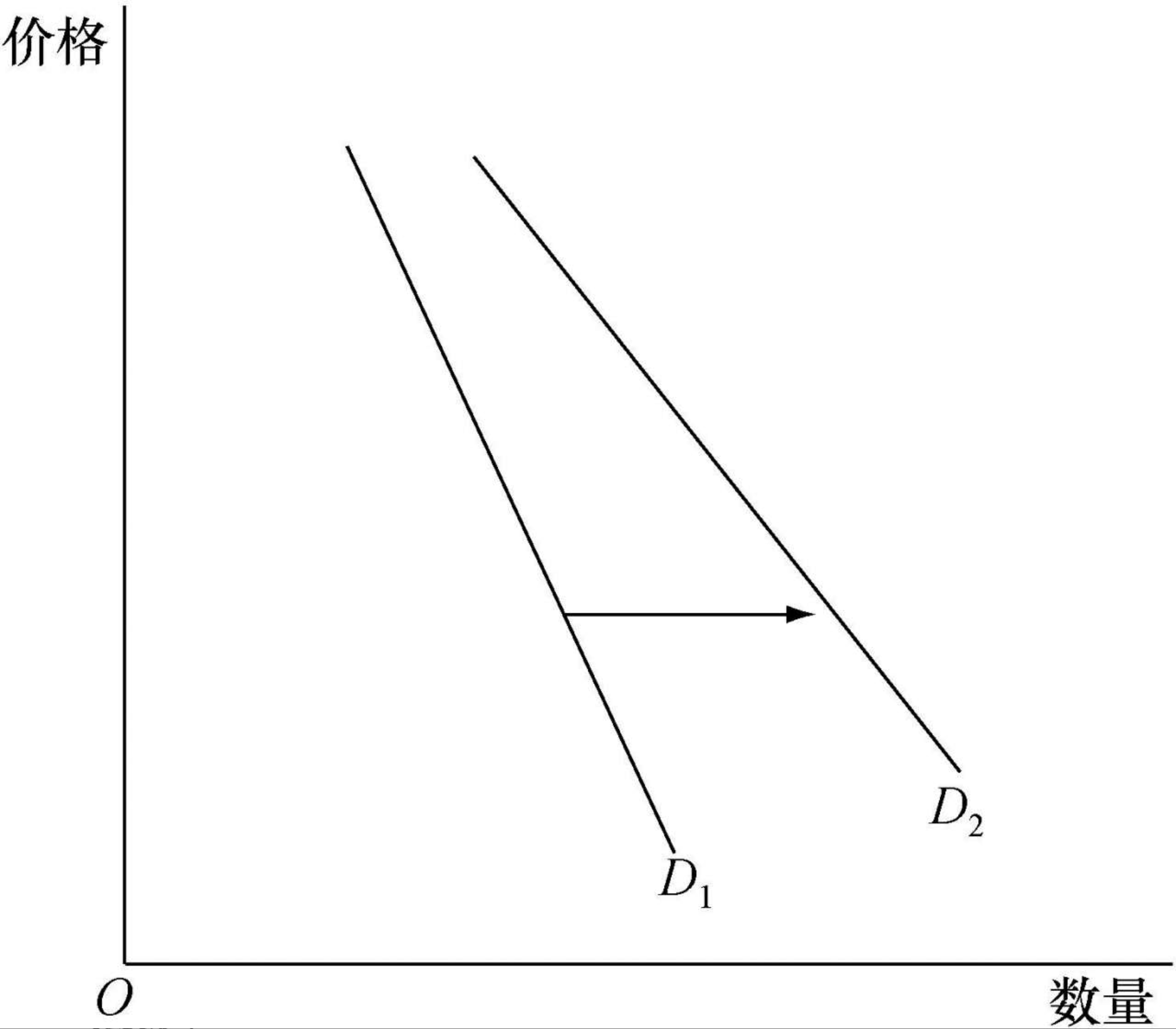
互补品:一种商品的价格上涨导致另一种商品的需求下降。
替代品价格上升,需求曲线向右移动,即对本商品的需求增加了。
互补品价格上升,需求曲线向左移动,即对本商品的需求减少了。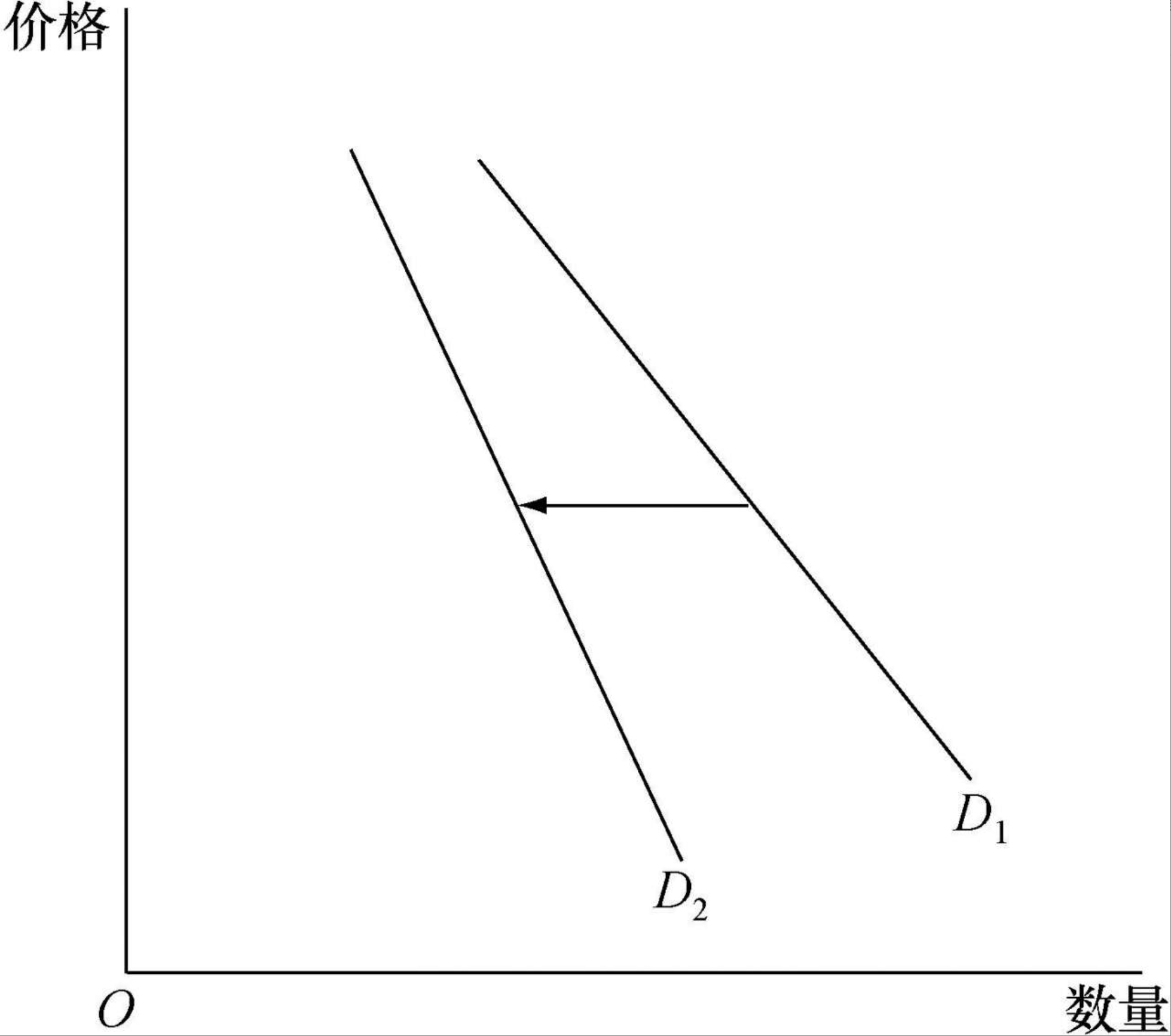
4.3.3 消费者剩余
在开放市场当中,交易都是自愿的,每个消费者付出的代价不会大于他得到的收益,否则交易就不太可能进行,因此,交易一定会给消费者带来至少大于零的消费者剩余。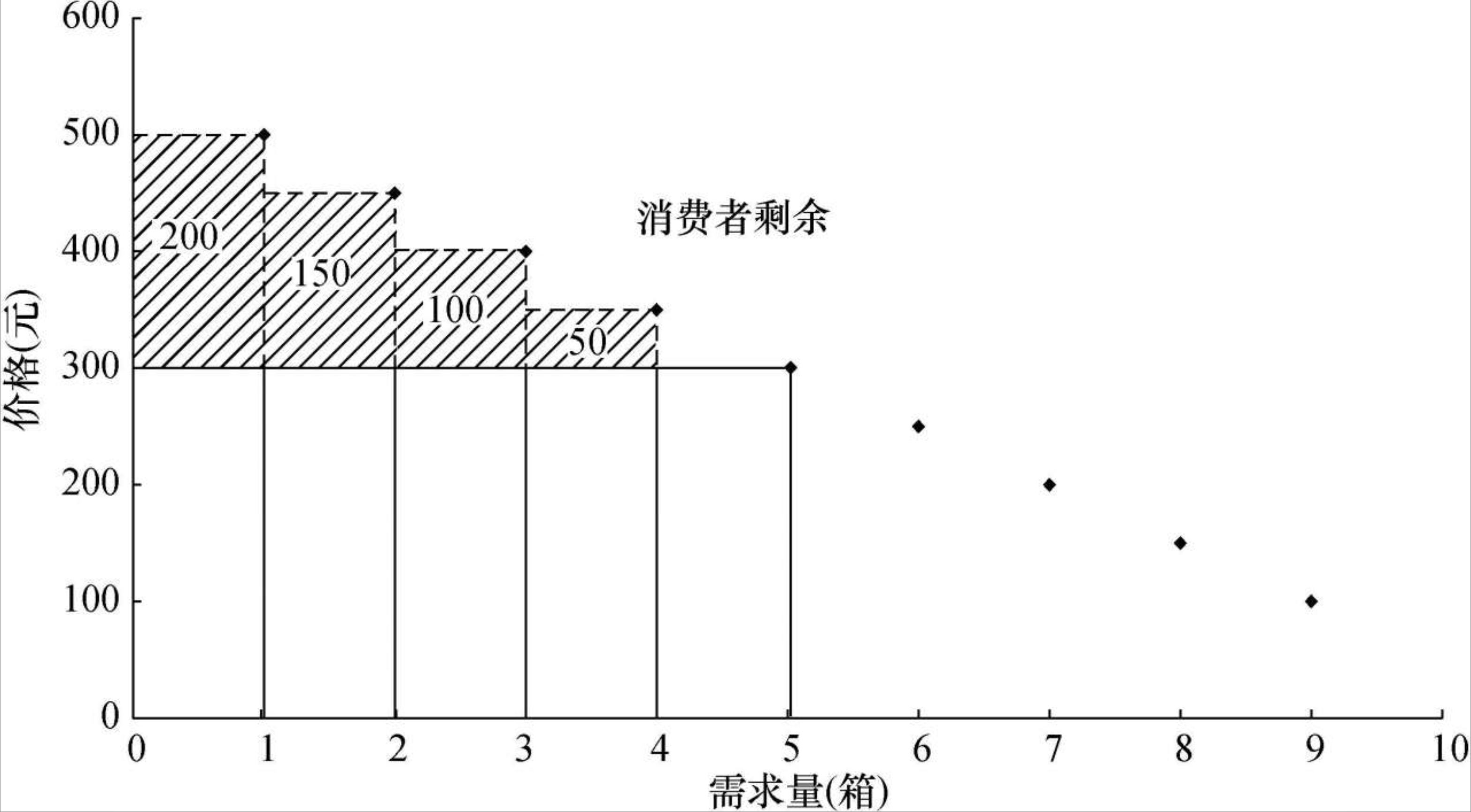
消费者剩余:消费者宁愿付出而不愿意得不到此物的最大价格与消费者为此物实际支付的价格之间的差额。消费者剩余是纵坐标、需求曲线和价格水平线围成的区间。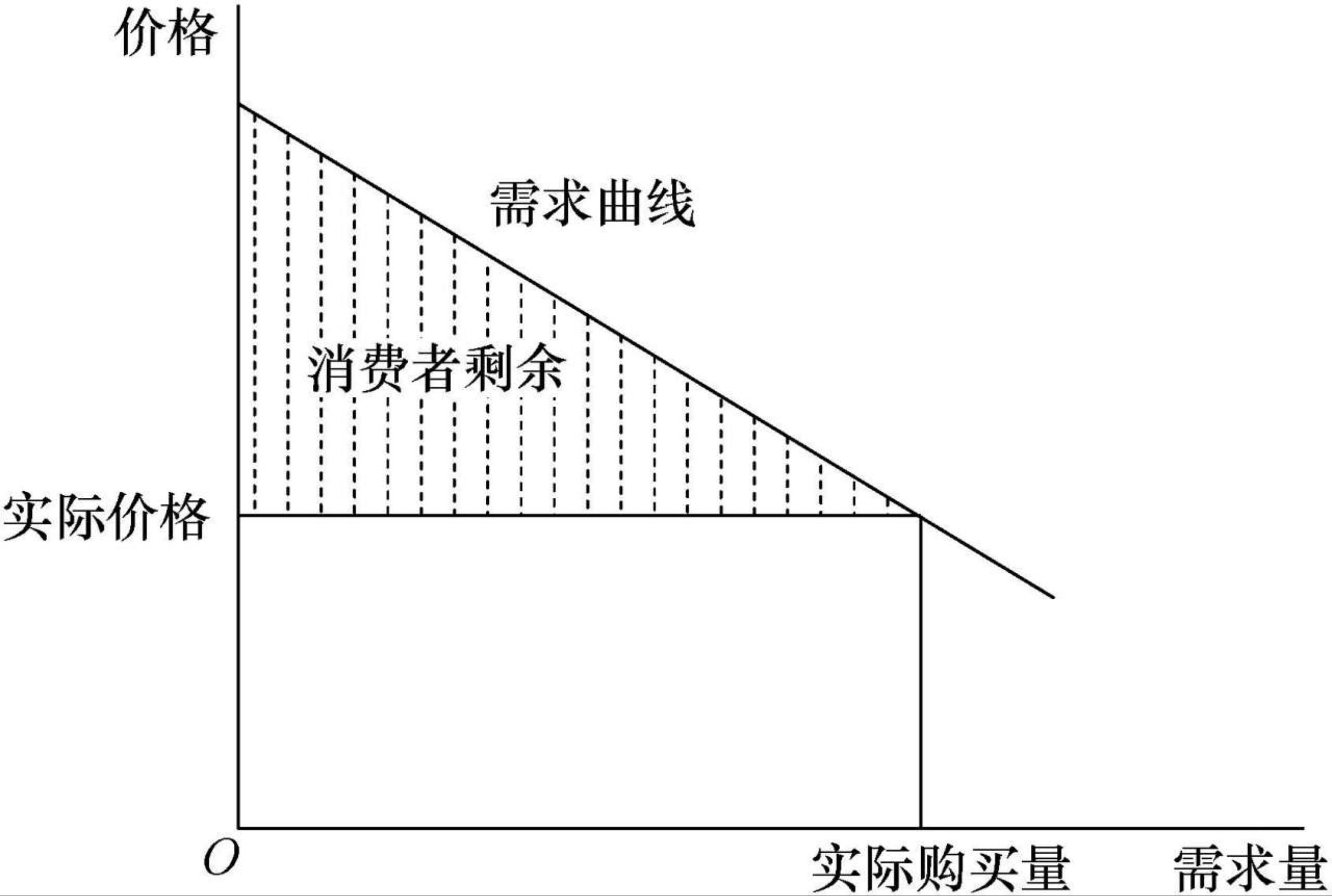
在市场中,谁给消费者带来的消费者剩余多,谁就能够获胜。
企业的直接目标是利润,但是前提是要给消费者带来幸福。
这就是为什么可以把市场的逻辑概括成一句话:你要过得幸福,首先要给别人带来幸福。
4.4 需求弹性
4.4.1 需求的价格弹性
需求的价格弹性:需求量变化的百分比与价格变化的百分比的比值。
公式:
$$需求价格弹性 = \frac{需求变化的百分比}{价格变化的百分比}=\frac{\Delta D/D }{\Delta p/p} $$
自价格弹性:衡量自身价格变化的需求弹性。
交叉价格弹性:衡量其他产品(替代品或互补品)价格变化的需求弹性。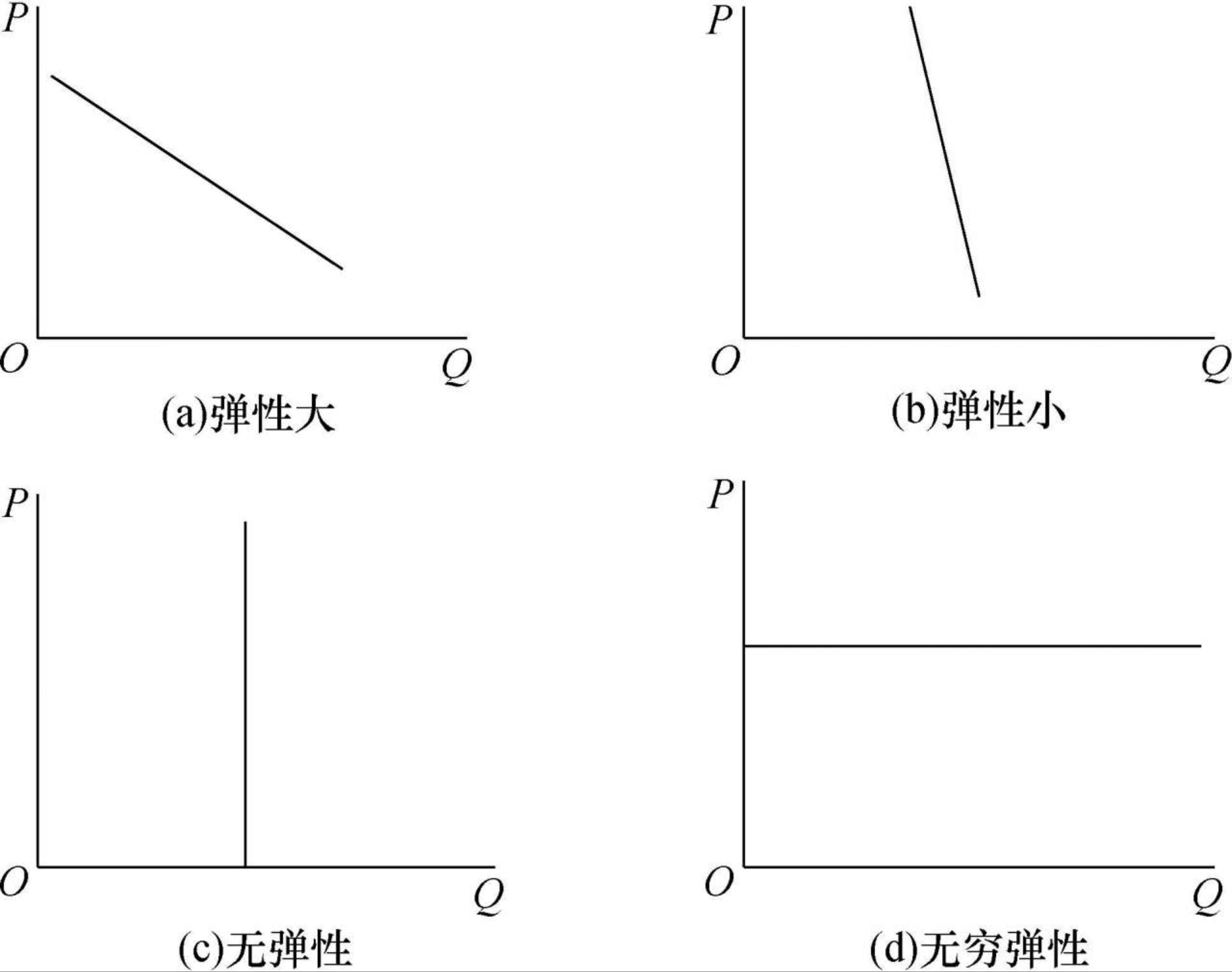
于一条线性的需求曲线而言,其任何一点对应的斜率是相同的,但是每一点的弹性是不同的。从左至右,弹性从无穷大逐渐下降至零。
需求函数为$D=a-bP$,$EP$表示需求价格弹性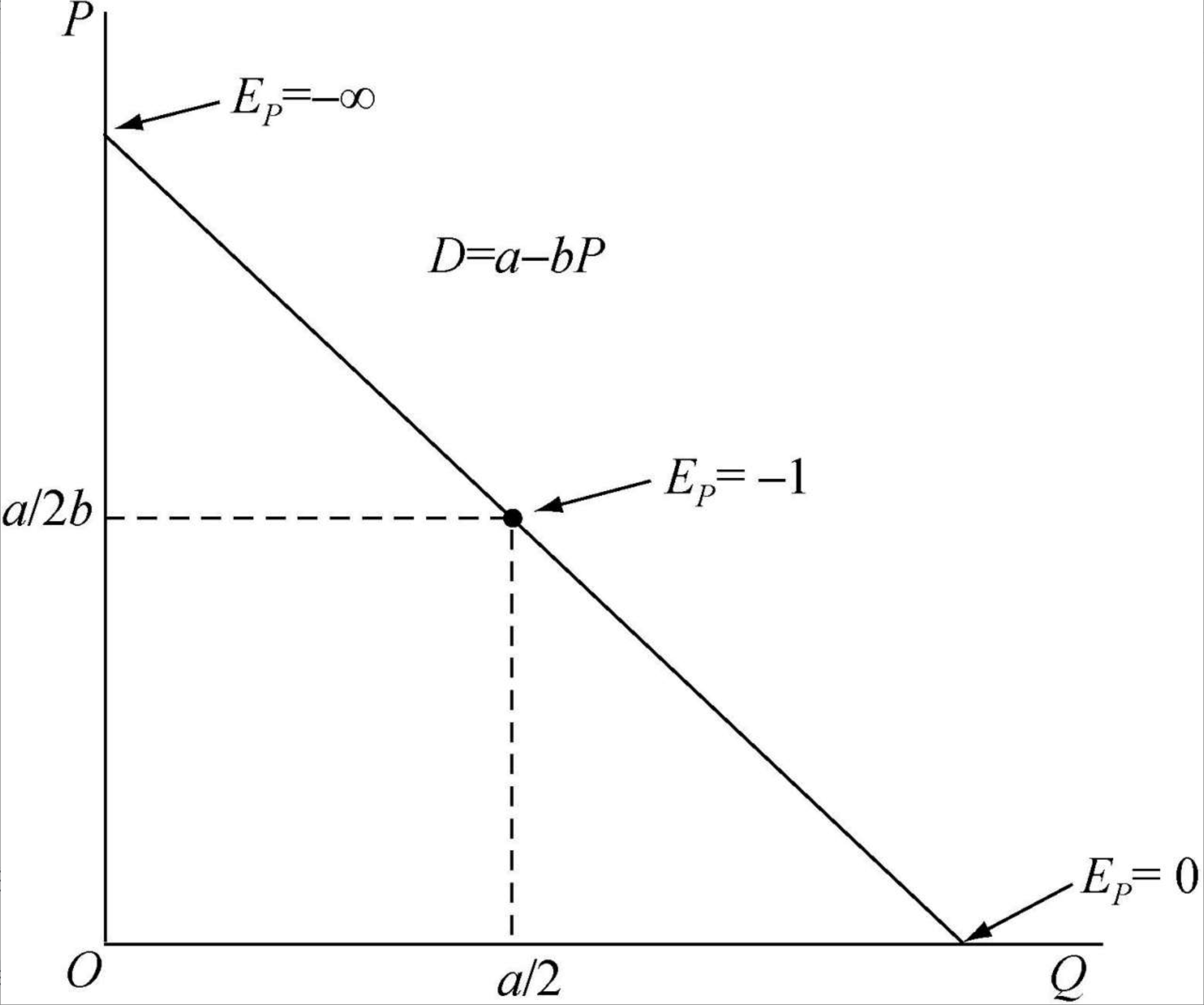
如果需求曲线是一条指数幂函数曲线$D=P^{-λ}$ ,价格弹性λ与价格水平无关。
价格弹性不变的需求曲线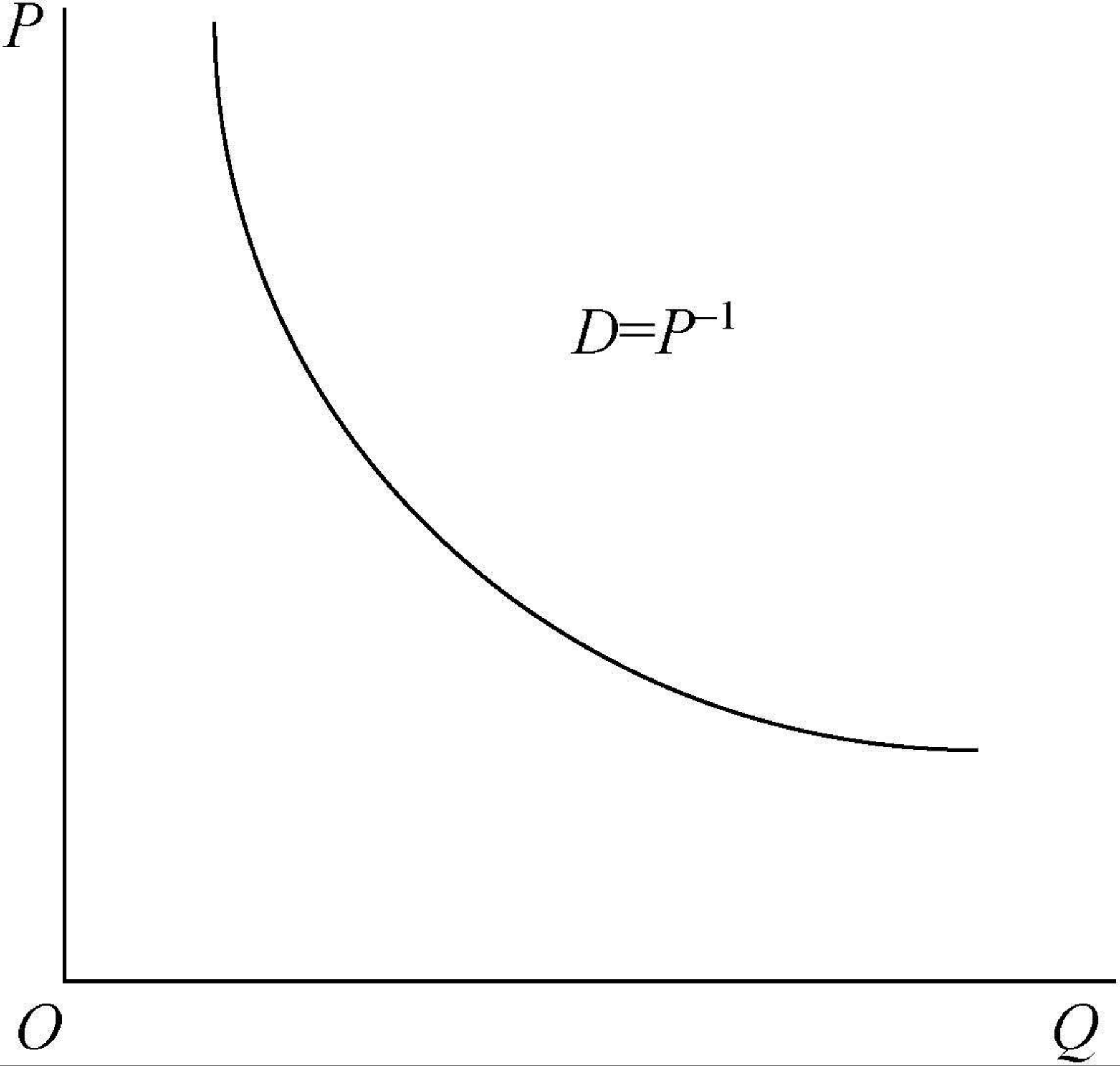
弧弹性与价格弹性的中点法
传统点弹性公式的缺陷:当某地区苹果价格从6元/斤下降到3元/斤的时候,根据需求曲线我们可以预期该地区苹果的需求量将会从50吨上升到75吨,此时价格下降了50%,需求上升了50%,根据点弹性的公式,计算出的弹性值为1;反之,当苹果价格从3元/斤上涨到6元/斤时,其需求量将会从75吨下降到50吨,此时价格上涨了100%,需求下降了33%,计算出的弹性值为0.33。这样,在需求曲线的同一区间上得出了两个不同的弹性值。
之所以出现这个问题,主要是因为在上例中的两种情况下,点弹性计算所选取的需求量D和价格p是不同的,因而得到的数值也不相同。
价格弹性的中点法:$需求价格弧弹性=\frac{\Delta D/\bar{D} }{\Delta p/\bar{p} } =\frac{D_2-D_1/[(D_1+D_2)/2]}{p_2-P_1/[(p_1+p_2)/2]}$
影响价格弹性的主要因素:
- 价格弹性的大小取决于该产品支出在总收入中所占的比例。这个比例越小,需求的价格弹性越小
- 价格弹性的大小取决于替代品的多少。通常替代品越多,商品涨价将导致消费者转而选择其替代品,因此商品对应的需求弹性越大;反之,替代品越少,需求弹性越小。
- 价格弹性取决于产品的耐久性。商品耐久性越高,价格弹性越大。对耐久性商品,消费者会更愿意根据价格变化的预期调整购买时点。
- 商品的属性也会影响其价格弹性的大小。必需品的价格弹性比较小,奢侈品的价格弹性比较大。
4.4.2 需求的收入弹性
收入弹性:需求变化率与收入变化率的比值,反映的是需求对消费者的收入变化的敏感度。
公式:$$需求收入弧弹性=\frac{需求变化的百分比}{收入变化的百分比} =\frac{\Delta D/D }{\Delta M/M } $$
恩格尔系数(衡量家庭和社会的富裕程度):必需品支出占总消费支出的比重衡量一个人的富裕程度或一个社会的整体富裕程度。一个人越富裕,一个社会越发达,必需品支出占总支出的比重越低。
- 59%以上:贫困
- 50%~59%:温饱
- 40%~50%:小康
- 30%~40%:富裕
- 低于30%:最富裕
4.5 需求的加总和市场
4.5.1 市场需求曲线
市场需求曲线:个体需求曲线的水平加总;总需求量随价格的下降而上升。
假设某种商品市场上存在着N个消费者,他们的偏好和收入都相同,因此他们的个人需求曲线也是相同的。
假设每个人对于该商品的需求函数为$d(p)=a-bp$。那么对于任意给定的价格,市场的总需求量为$D=Nd=N(a-bp)$
其中第$i$个消费者的个人需求函数为$di(p)$,那么市场的总需求函数变成$D=\sum_{i=1}^{N}d_i(p)$,可见,所有的市场总需求都可以通过个人需求的水平加总得到。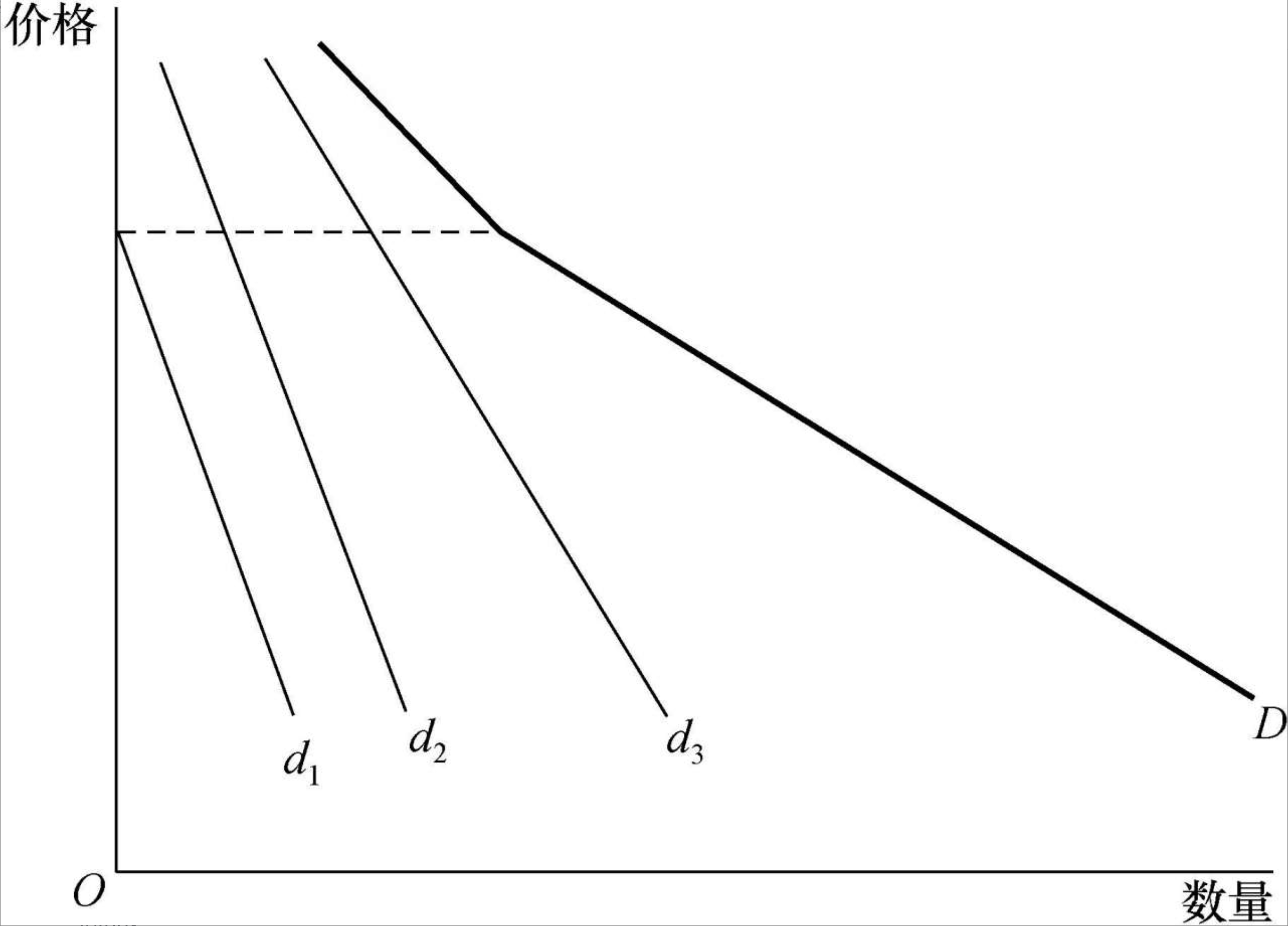
市场总需求增加的两类情况:
- 当商品价格下跌时,原有消费者根据各自的个人需求曲线增加个人的消费数量。
- 商品价格下跌,可能使市场上的消费者数量增加。有些人本来不会消费该商品,但是由于其价格的下降,转而开始选择消费该商品。
即单个消费者的需求是不连续的,甚至只是一个点,但市场的需求曲线仍然可能是连续的。如果商品对于所有消费者而言都不是吉芬商品,那么价格的变动将导致所有消费者决策向着同一个方向移动,进而可以推断出市场总需求对于价格的变动将更加敏感。通常来说,市场需求的价格弹性要大于消费者个体需求的价格弹性,也就是市场的总需求曲线更加平坦。
4.5.2 经济发展的度量
奢侈品的必需品化来自两个因素:
- 收入水平的提高
- 价格的下降
而这两个因素又来自一个共同因素的作用,这就是创新和技术进步。创新和技术进步不断提高劳动生产率,一方面降低了生产成本,导致价格下降,另一方面增加了消费者的收入。
哈耶克: - 在一种新商品成为一种公众需要并构成一种生活必需品之前,通常只是少数人的玩物。因此,今日的奢侈品乃是明日之必需品,限制当前少数人的奢侈品消费,就等于阻止多数人今后的必需品消费。
- 富有者购买此类新商品支付的费用,有一部分被用来支付试验新产品的费用(尽管富有者的目标并不在此),而作为这一进程的结果,这些物品便可以在晚些时候为贫穷者所享用。
1990—2010年桑塔纳轿车的价格变化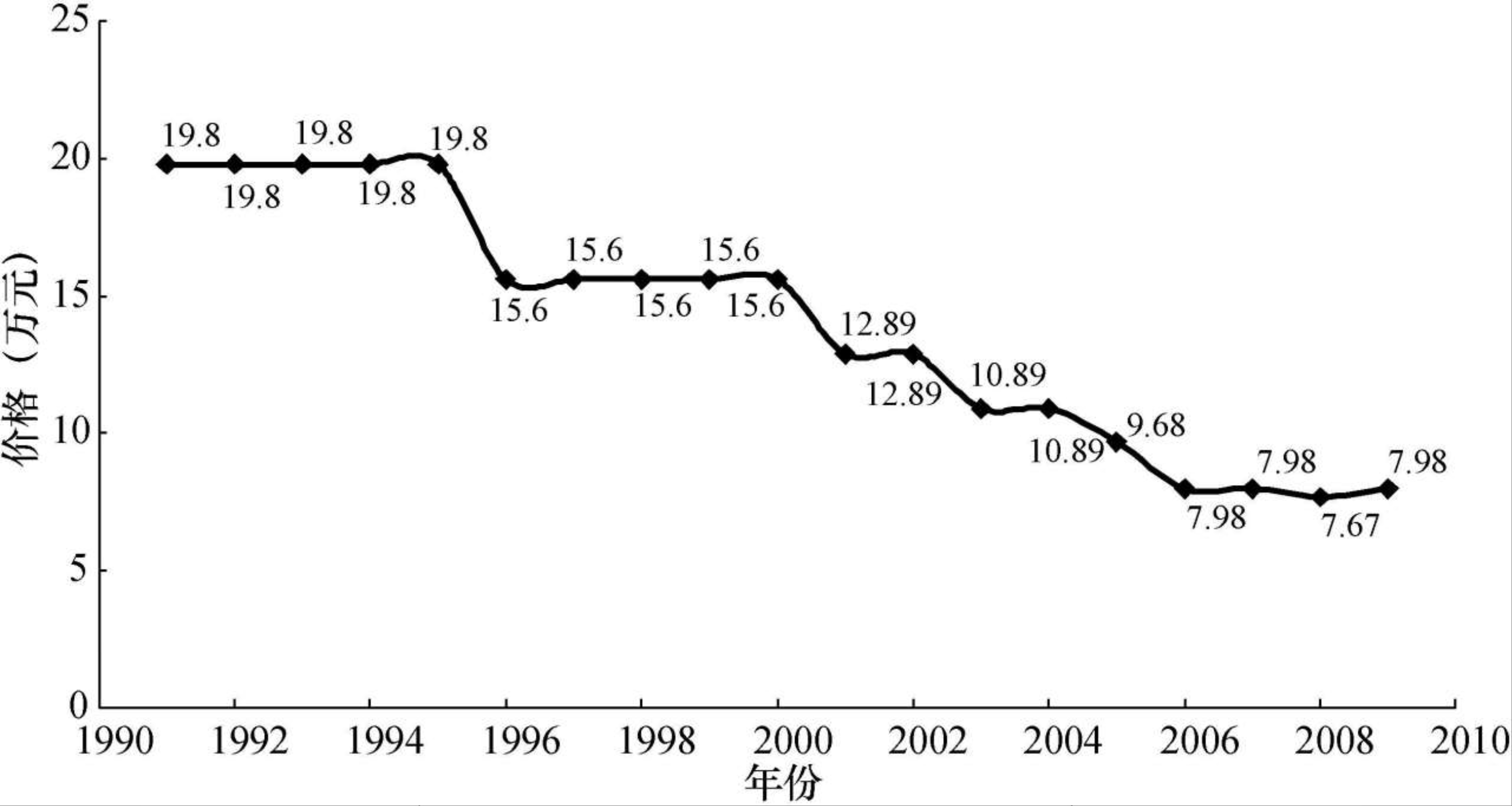 [img-caption:: 化肥投入与玉米产量的对应关系]
[img-caption:: 化肥投入与玉米产量的对应关系]
1997—2011年中国汽车保有量的变迁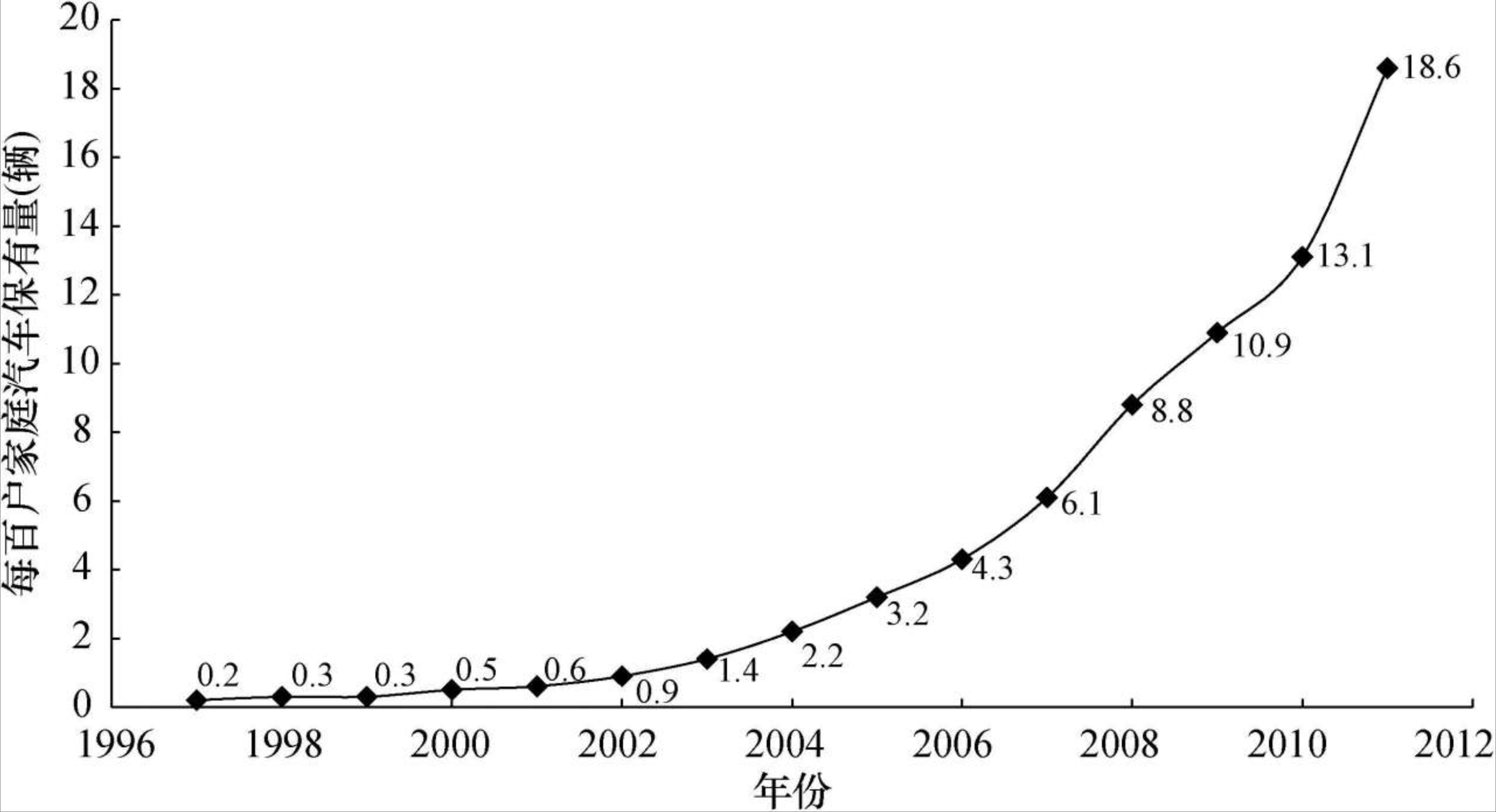
第5章 生产与供给曲线
5.1 生产技术
5.1.1 生产函数
生产函数:投入与产出之间的关系。 $y=f(x_1,x_2,…,x_n)$,y代表某种产品的产量,$x_i$代表第i种要素的投入量。
短期:只有一种或部分要素投入可变的时间跨度。
长期:所有要素投入都可以改变的时间跨度。
5.1.2 短期生产函数
1 | [img-caption:: 化肥投入与玉米产量的对应关系 单位:10千克] |
要素的平均产量:总产量除以投入总量 $AP=\frac{y}{x}$
要素的边际产量:增加一单位的要素投入所增加的产出量 $MP=\frac{\mathrm{d} y}{\mathrm{d} x}$
1 | [img-caption:: 总产量、平均产量和边际产量 单位:10千克] |
边际生产率递减法则的表现:平均产量、际产量随着要素投入的增加不断下降,平均产量下降是边际产量下降的结果,这是因为新投入带来的产出数量低于原来的平均值,因此新的平均值被拉低了。
$$\begin{array}{c}
如果MP(X)<AP(X),那么有\
\
\frac{\mathrm{d} AP}{\mathrm{d} x}=\frac{\mathrm{d} TP/x}{\mathrm{d} x}=\frac{(xMP-TP)}{x^2} =\frac{(MP-AP)}{x^2}<0
\end{array} $$
1 | [img-caption:: 平均产量和边际产量图示] |
在土地等其他要素投入固定的情况下,每单位新增化肥所增加的玉米产量随着化肥投入的增加而递减。边际生产率递减法则适用于所有的要素投入,包括劳动、资本、土地等。
边际生产率递减法则:在其他要素投入不变、只有一种要素投入可变的情况下,可变要素投入超过一定的临界值后,其对应的边际产量随着投入的增加而下降。
马尔萨斯陷阱:由于边际生产率递减法则的作用,随着人口增多,人均粮食产量会越来越少,人类永远只能生活在生存线上,生活水平不可能提高。
马尔萨斯陷阱的缺陷:经济不仅受边际生产率递减法则的支配,也受技术进步的支配。如果技术进步速度足够快,边际生产率递减法则就不会表现为人均产出的减少,因为技术进步可以提高边际生产率。
5.1.3 长期生产函数
只有资本和劳动两种要素的情况下,生产函数变为: $y=f(K,L)$ ,K:资本;L:劳动。
- 资本在物质形态上表现为厂房、机器设备、中间品、原材料等。
- 劳动指劳动者的体力、知识、智力的投入。
- 劳动必须与资本结合才能生产出产品。
表中:随着劳动的增加,要保持原产出,资本的投入就可以相应减少,二者存在此消彼长的替代关系。
1 | [img-caption:: 生产相同产出量的不同要素投入组合] |
等产量曲线:表示某一固定产出下对应的所有投入组合的连线。
资本与劳动的可替代程度取决于等产量曲线的形状,是由技术决定的,与要素价格无关。
劳动对资本的边际技术替代率:沿着等产量曲线,每单位劳动可替代的资本投入 $MRTS_LK = -\frac{\Delta K }{\Delta L}$
劳动对边际技术替代率递减法则:随着劳动投入的增加,每单位劳动能替代的资本越来越少。
类似地,资本对劳动的边际技术替代率也是随着资本投入数量的增加而递减
边际技术替代率:在产量不变的前提下,增加一单位某种要素投入可以替代的另外一种要素的数量。
边际技术替代率递减法则:随着一种要素投入的增加,该要素可替代的其他要素的数量不断递减。
1 | [img-caption:: 边际替代率递减法则] |
5.1.4 规模报酬
规模报酬:当所有要素同比例增加时,产量如何变化。
1 | [img-caption:: ] |
柯布-道格拉斯生产函数(Cobb-Douglas production function):
$y = AK^\alpha L^\beta$ A:技术水平
- 如果两个指数之和等1: $y = AK^\alpha L^{1-\alpha}$ ,对应的技术是规模报酬不变的
- 如果两个指数相加大于1,规模报酬递增
- 如果两个指数相加小于1,规模报酬递减
5.2 生产成本
5.2.1 成本函数和成本曲线
成本函数: C=C(y),其中y表示产量。产量与为生产该产量而必须支付的最低成本之间的关系。
1 | [img-caption:: 成本函数和成本曲线] |
5.2.2 短期成本曲线
短期成本:只有一种要素投入或部分要素投入可变时的最低成本。
长期成本:指所有要素投入都可变时的最低成本。
固定成本(FC):在短期内,不随产量变化的成本;等于固定生产要素的支出。
可变成本(VC):随产量增减而变化的成本;等于可变生产要素的支出。
总成本(TC):固定成本和可变成本之和。
1 | [img-caption::玉米种植的固定成本、可变成本和总成本] |
平均成本:总成本与总产量之比。$AC=TC/y$
平均固定成本:固定成本与总产量之比。$AFC=FC/y$
平均可变成本:可变成本与总产量之比。$AVC=VC/y$
边际成本:增加一单位产出所增加的总成本。$MC=ΔTC/Δy$。
由于固定成本不随产量而增加,即边际固定成本是零,因此,边际成本等于边际可变成本。
当平均成本高于边际成本时,平均成本随着产量的增加而降低。
当平均成本低于边际成本时,平均成本随着产量的增加而上升。
边际成本曲线与平均总成本曲线和平均可变成本曲线一定相交于平均总成本曲线和平均可变成本曲线的最低点。
1 | [img-caption:: 平均成本与边际成本] |
5.2.3 长期成本曲线
长期成本中,所有的要素投入都是可变的。
假定要素投入分为资本和劳动两大类: $C=Kr+Lw$ K:资本投入 L:劳动投入 r:资本的价格 w:劳动力的价格
劳动力价格为1.2时,最优劳动-资本组合是3∶5.6;而当劳动力价格下降为0.8时,最优资本-劳动组合是5∶3.6
1 | [img-caption::不同价格下的最优投入组合] |
(a)给出了三条等成本曲线,越靠近原点的等成本线对应的成本越低;反之,越远离原点的等成本线对应的成本越高。由于要素价格是给定的,不同的等成本曲线一定是平行的。
(b)给出了当产量为y时的等产量曲线。把等产量曲线和等成本曲线放在一起,我们就得到了图(c)。
企业的问题是:如何选择投入组合,用最低的成本生产出给定的产量y。
(c)生产产量y1成本最低的要素投入组合点是A点。过A点的等成本曲线上的其他组合给出相同的成本,但生产不出所要求的产量y1;这条等成本曲线以内的组合给出更低的成本,但同样生产不出所要求的产量y1;这条等成本曲线以外的组合有可能生产出所要求的产量y1,但不是成本最低的组合。
1 | [img-caption:: 成本最小化问题] |
最优组合点A满足这样的条件:等产量曲线的要素边际替代率(绝对值)等于要素价格比率 $$\frac{\Delta K}{\Delta L}=\frac{\partial y/\partial L}{\partial x/\partial K}=\frac{w}{r}$$
最优组合的最后一单位的成本支出不论花在资本投入上还是劳动投入上,其边际产量是相同的。如果最后一单位成本支出,资本的边际生产率大于劳动的边际生产率,通过用资本替代劳动就可以降低成本支出。
成本最低的要素组合依赖于要素的相对价格。
最优要素组合的数学分析
数学上,给定产量下成本最小化可以表示为求解如下最优化问题:
$$\begin{array}{}
min(Kr+Lw)\
s.t.y≤f(K,L)
\end{array}{} $$
构建拉格朗日函数:$l=Kr+Lw+λ(y-f(K,L))$
分别就K和L对l求导,令两个一阶导数等于零,可知最优解(K,L)满足如下一阶条件:
$$\frac{\partial f/\partial K}{r}=\frac{\partial f/\partial L}{w}=\frac{1}{\lambda }$$
得到等成本线的斜率$-\frac{w}{r}$等于等产量线的斜率(要素在技术上的边际替代率):
$$MRTS_{LK}=\frac{\mathrm{d} K}{\mathrm{d} L} = -\frac







